3.
\(u_2=\dfrac{1}{2-u_1}=\dfrac{1}{2-\dfrac{1}{2}}=\dfrac{2}{3}\)
\(u_3=\dfrac{1}{2-u_2}=\dfrac{1}{2-\dfrac{2}{3}}=\dfrac{3}{4}\)
\(u_4=\dfrac{1}{2-\dfrac{3}{4}}=\dfrac{4}{5}\)
4.
\(u_1=\dfrac{2^{1+1}+1}{2^1}=\dfrac{5}{2}\)
\(u_3=\dfrac{2^4+1}{2^3}=\dfrac{17}{8}\)
\(u_5=\dfrac{2^6+1}{2^5}=\dfrac{65}{32}\)
5. Đề bị khuất
Câu 2: Chọn A.
Câu 3: Chọn B.
Câu 4: Chọn C.
Bạn đã yêu cầu Câu 5, hình bị mất một phần câu 5! Bạn kiểm tra giúp mình!
5.
\(\dfrac{2n}{n^2+1}=\dfrac{9}{41}\Rightarrow9n^2+9=82n\)
\(\Rightarrow9n^2-82n+9=0\Rightarrow\left[{}\begin{matrix}n=9\\n=\dfrac{1}{9}\notin Z\left(loại\right)\end{matrix}\right.\)
Vậy đó là số hạng thứ 9
6.
\(u_{n+1}=2u_n+3\Leftrightarrow u_{n+1}+3=2\left(u_n+3\right)\)
Đặt \(u_n+3=v_n\Rightarrow\left\{{}\begin{matrix}v_1=u_1+3=4\\v_{n+1}=2v_n\end{matrix}\right.\)
\(\Rightarrow v_n\) là cấp số nhân với công bội \(q=2\)
\(\Rightarrow v_n=v_1.q^{n-1}=4.2^{n-1}=2^{n+1}\)
\(\Rightarrow u_n=v_n-3=2^{n+1}-3\) (hoặc \(2.2^n-3\))








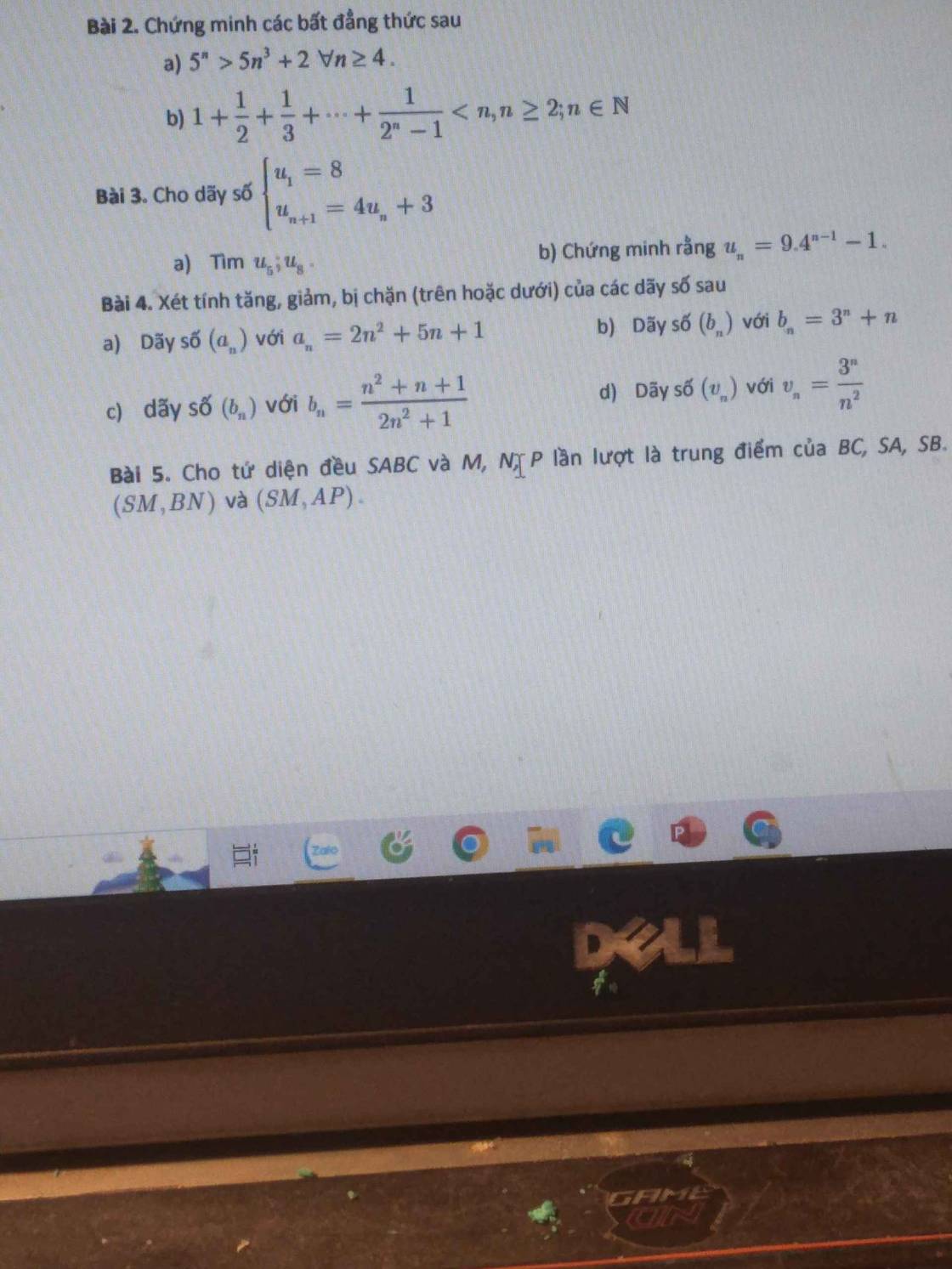 giúp em xét đãy số bị chặn của bài 4 với ạ. cần gấp ạ. Em cảm ơn ạ
giúp em xét đãy số bị chặn của bài 4 với ạ. cần gấp ạ. Em cảm ơn ạ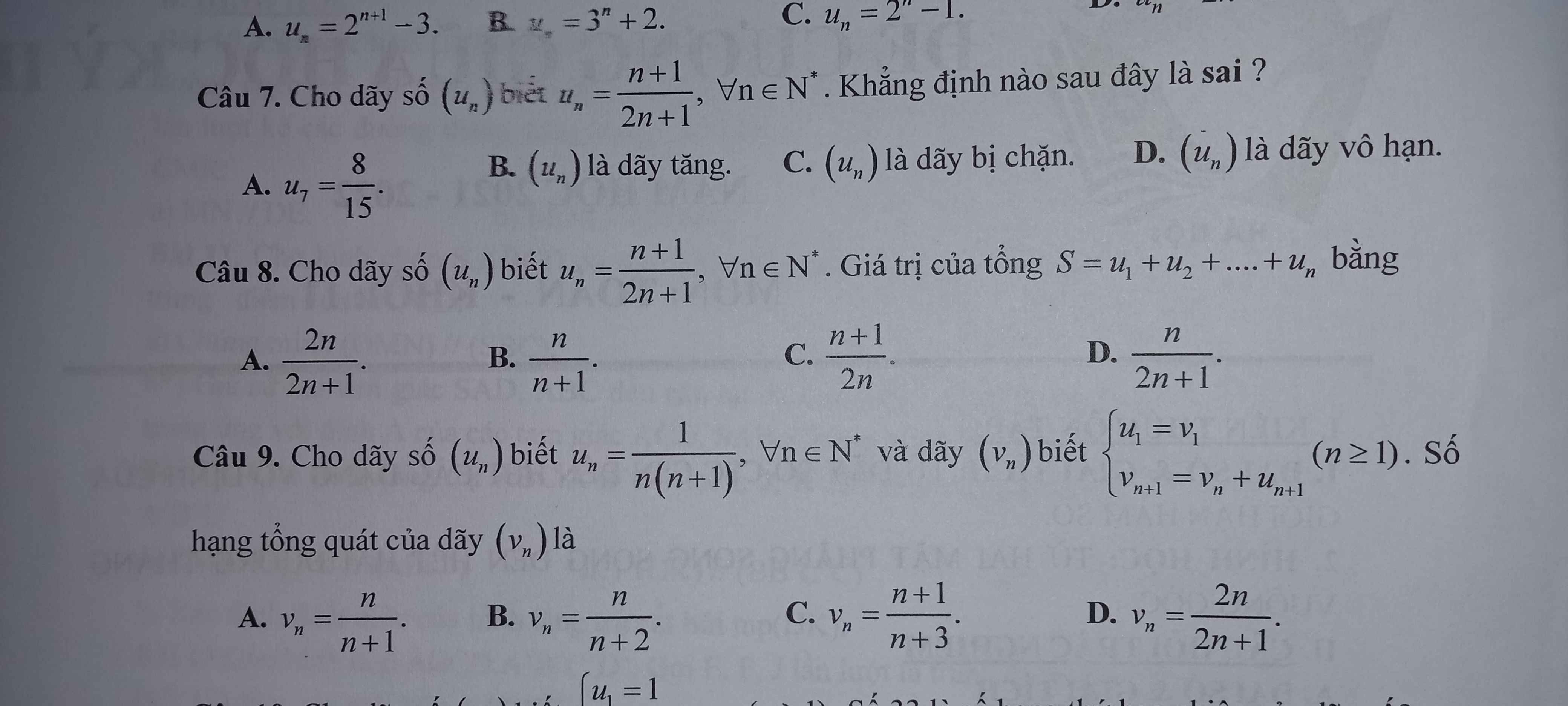





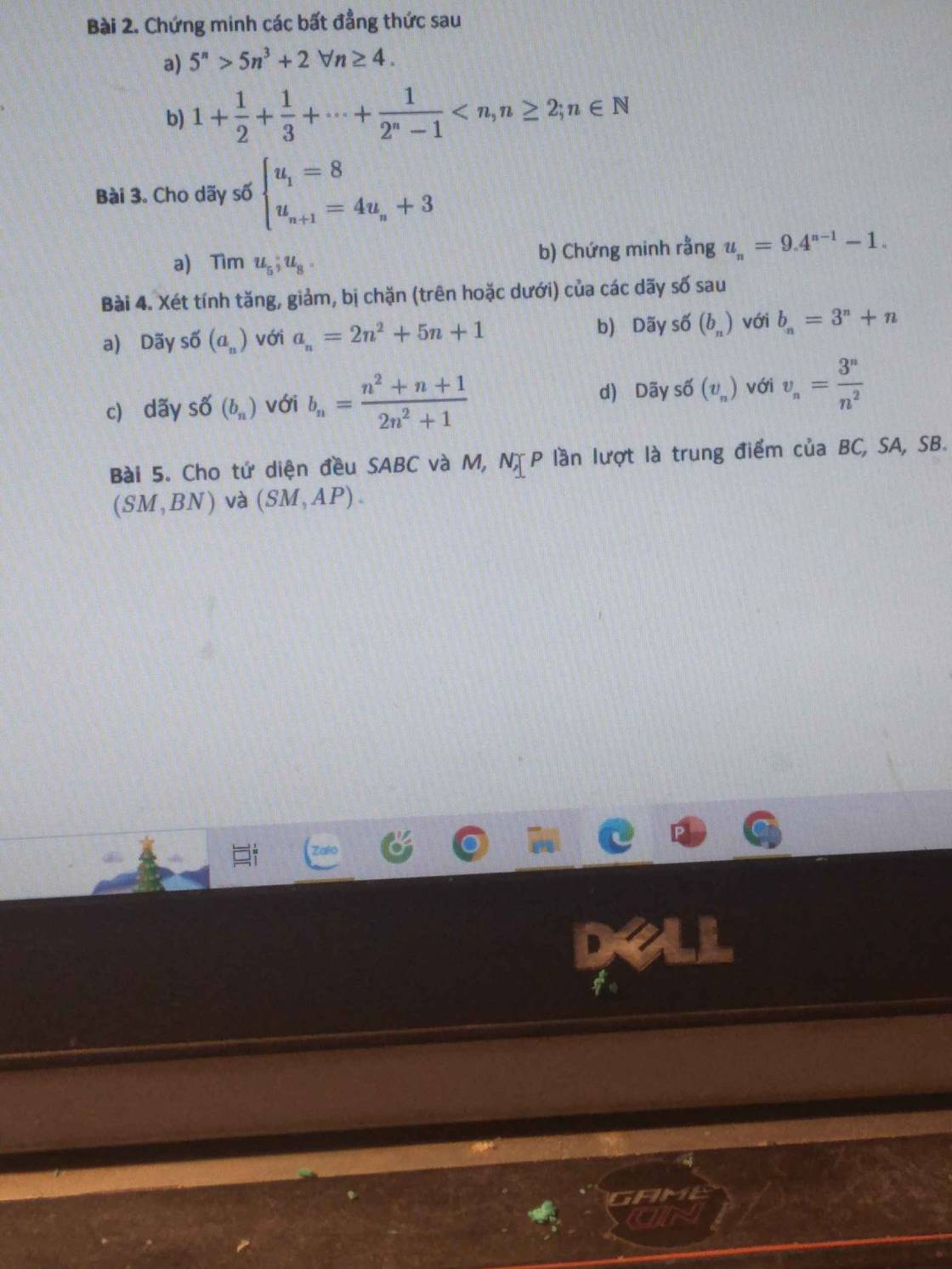 giúp em bài 4 với ạ. Pls
giúp em bài 4 với ạ. Pls
