7.
\(u_1=\dfrac{1+1}{2.1+1}=\dfrac{2}{3}\) ; \(u_2=\dfrac{2+1}{2.2+1}=\dfrac{3}{5}\Rightarrow u_1-u_2=\dfrac{2}{3}-\dfrac{3}{5}=\dfrac{1}{15}>0\)
\(\Rightarrow\) Dãy đã cho là dãy giảm nên đáp án B sai
8.
Đề bài sai, rõ ràng \(u_1+u_2>1\) nhưng tất cả công thức trong dãy đều cho tổng nhỏ hơn 1
9.
\(u_{n+1}=\dfrac{1}{\left(n+1\right)\left(n+2\right)}\); \(v_1=u_1=\dfrac{1}{2}\)
\(v_{n+1}=v_n+\dfrac{1}{\left(n+1\right)\left(n+2\right)}=v_n+\dfrac{1}{n+1}-\dfrac{1}{n+2}\)
\(\Rightarrow v_{n+1}+\dfrac{1}{\left(n+1\right)+1}=v_n+\dfrac{1}{n+1}\)
Đặt \(v_n+\dfrac{1}{n+1}=x_n\Rightarrow\left\{{}\begin{matrix}x_1=v_1+\dfrac{1}{2}=1\\x_{n+1}=x_n=...=x_1=1\end{matrix}\right.\)
\(\Rightarrow v_n+\dfrac{1}{n+1}=1\Rightarrow v_n=1-\dfrac{1}{n+1}=\dfrac{n}{n+1}\)

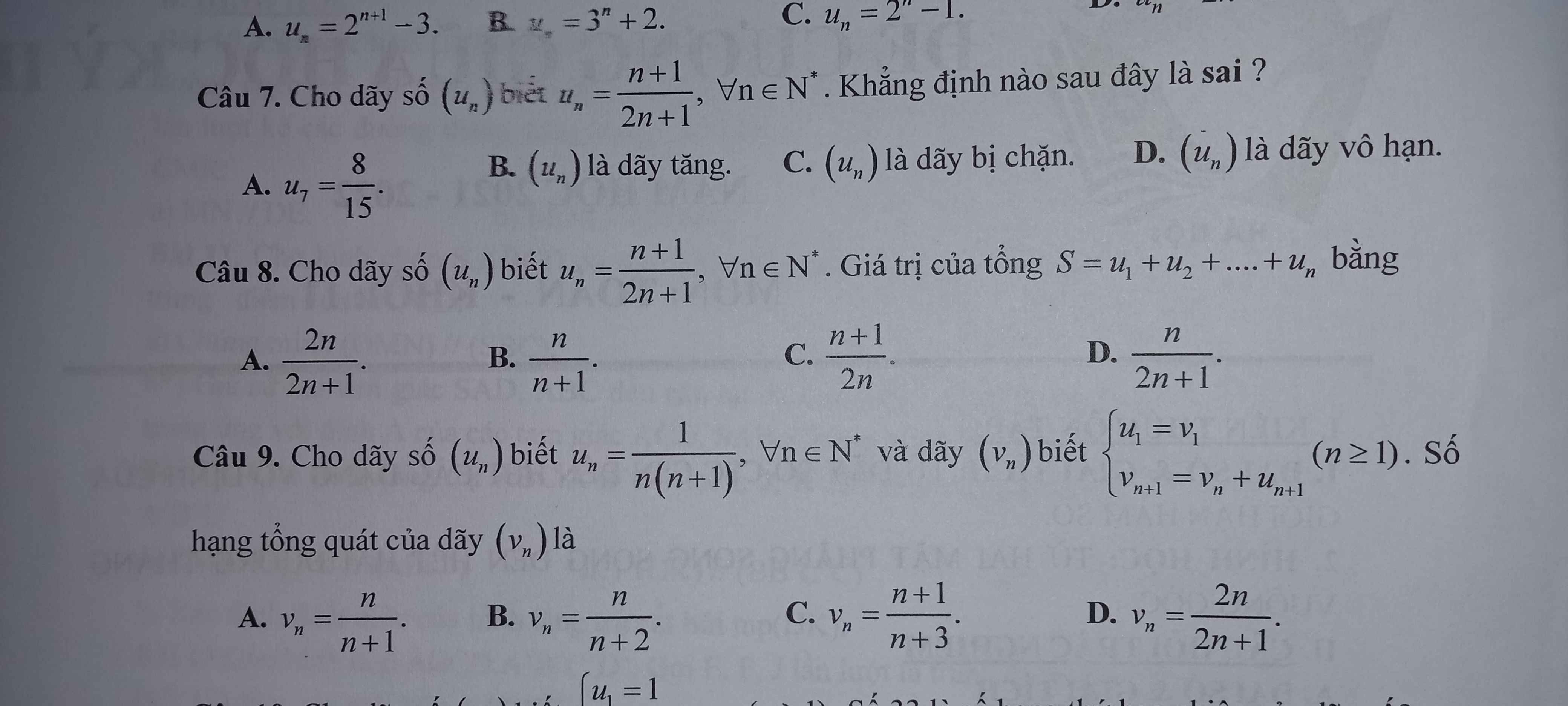





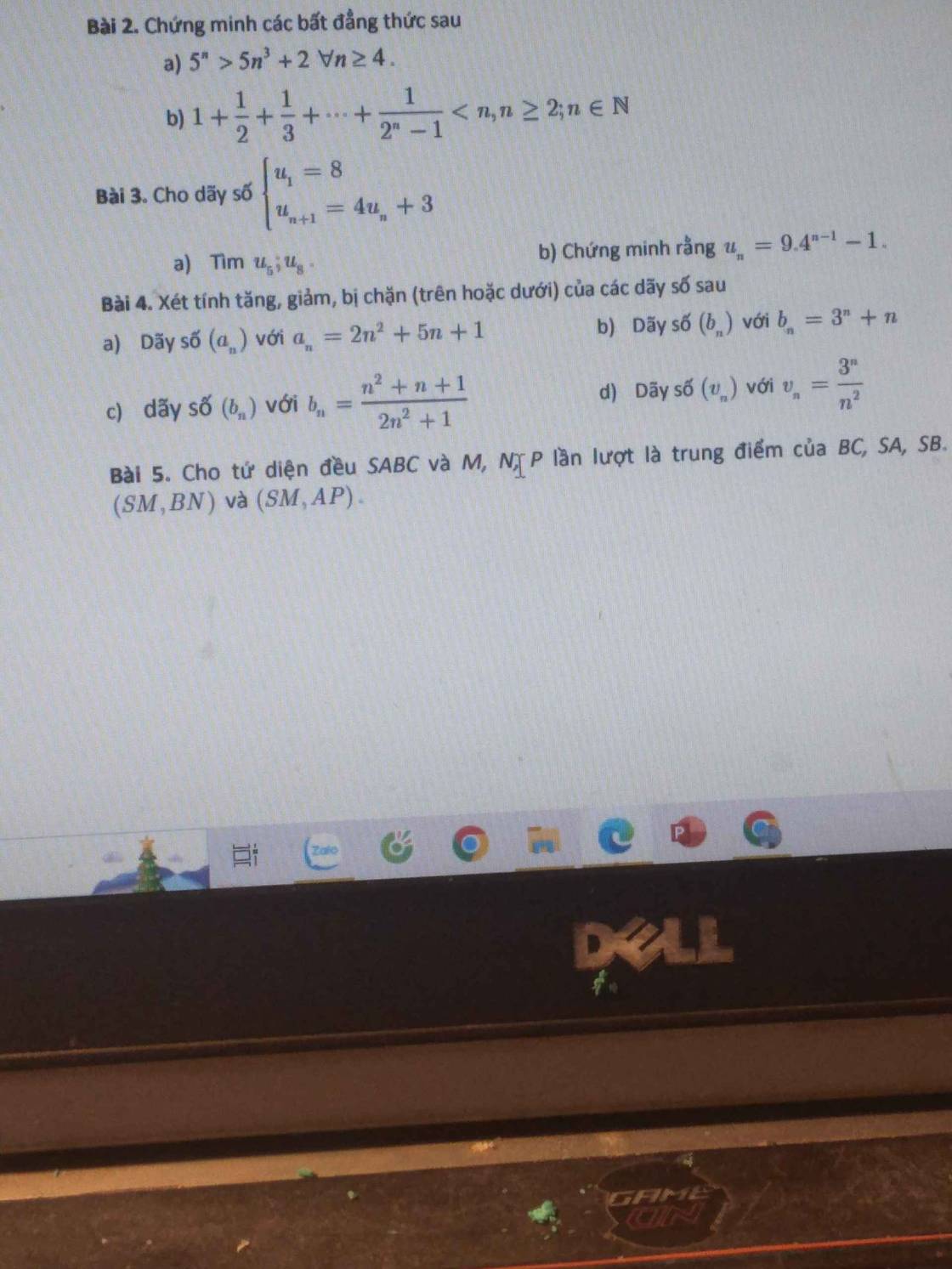 giúp em xét đãy số bị chặn của bài 4 với ạ. cần gấp ạ. Em cảm ơn ạ
giúp em xét đãy số bị chặn của bài 4 với ạ. cần gấp ạ. Em cảm ơn ạ



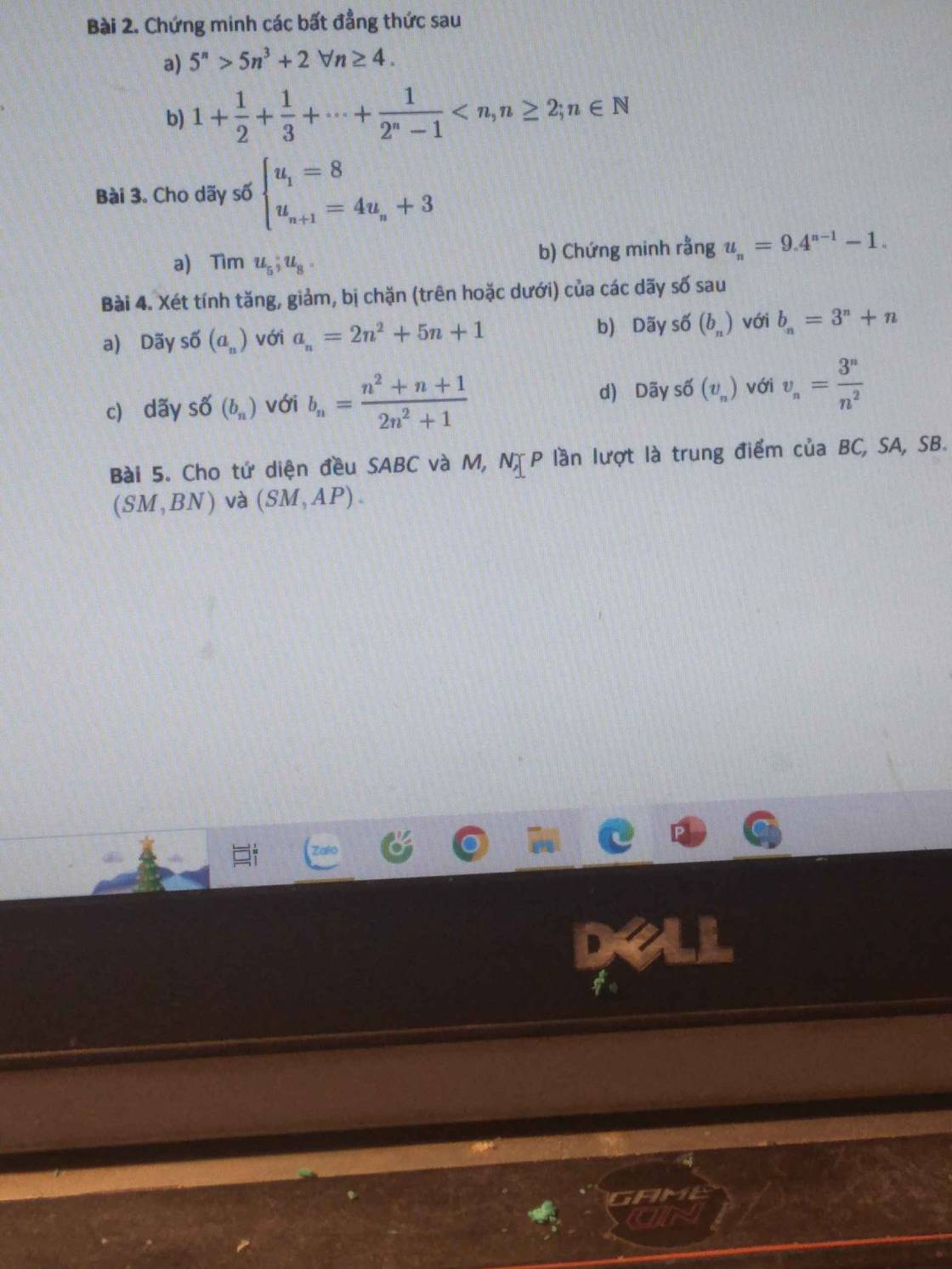 giúp em bài 4 với ạ. Pls
giúp em bài 4 với ạ. Pls

