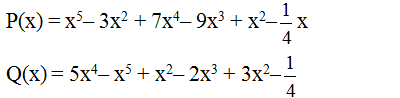Question

Các pn cho mk hỏi chút nhé!

Cho hai đa thức:

a) Thu gọn và sắp xếp hai đa thức P(x) và Q(x) theo lũy thừa giảm của biến.

b) Tính: P(x) + Q(x) và P(x) – Q(x)

c) Chứng minh rằng x=1 là nghiệm của đa thức Q(x) nhưng không là nghiệm của đa thức P(x).

Answer 1

a) P(x) = 3x²+2x³+2x+5-x²-x

=2x³+3x²-x²-x+5

=2x³+2x²+x+5

Q(x) = x³-2x-2+3x-x²+1

=x³-x²-2x+3x-2+1

= x³-x²+x-1

Answer 2

a) \(P\left(x\right)=2x^2+2x^3+x\)

\(Q\left(x\right)=x^3+x-1-x^2\)

Sắp xếp theo lũy thừa giảm của biến ta có:

\(P\left(x\right)=2x^3+2x^2+x\)

\(Q\left(x\right)=x^3-x^2+x-1\)

b) \(P\left(x\right)+Q\left(x\right)=3x^3+x^2+2x-1\)

\(P\left(x\right)-Q\left(x\right)=x^3+3x^2+1\)

c) Thay x=1 vào đa thức Q(x), ta có:

\(Q\left(1\right)=1^3-1^2+1-1=0\)

Vậy x=1 là nghiệm của đa thức Q(x) (*)

Thay x=1 vào đa thức P(x), ta có:

\(P\left(1\right)=2.1^3+2.1^2+1=5\)

=> x=1 k phải là nghiệm của đa thức P(x) (**)

Từ (*) và (**) => (đpcm)

Answer 3

Làm nãy giờ lỡ tay bấm quay lại 1 cái ==' :3

Answer 4