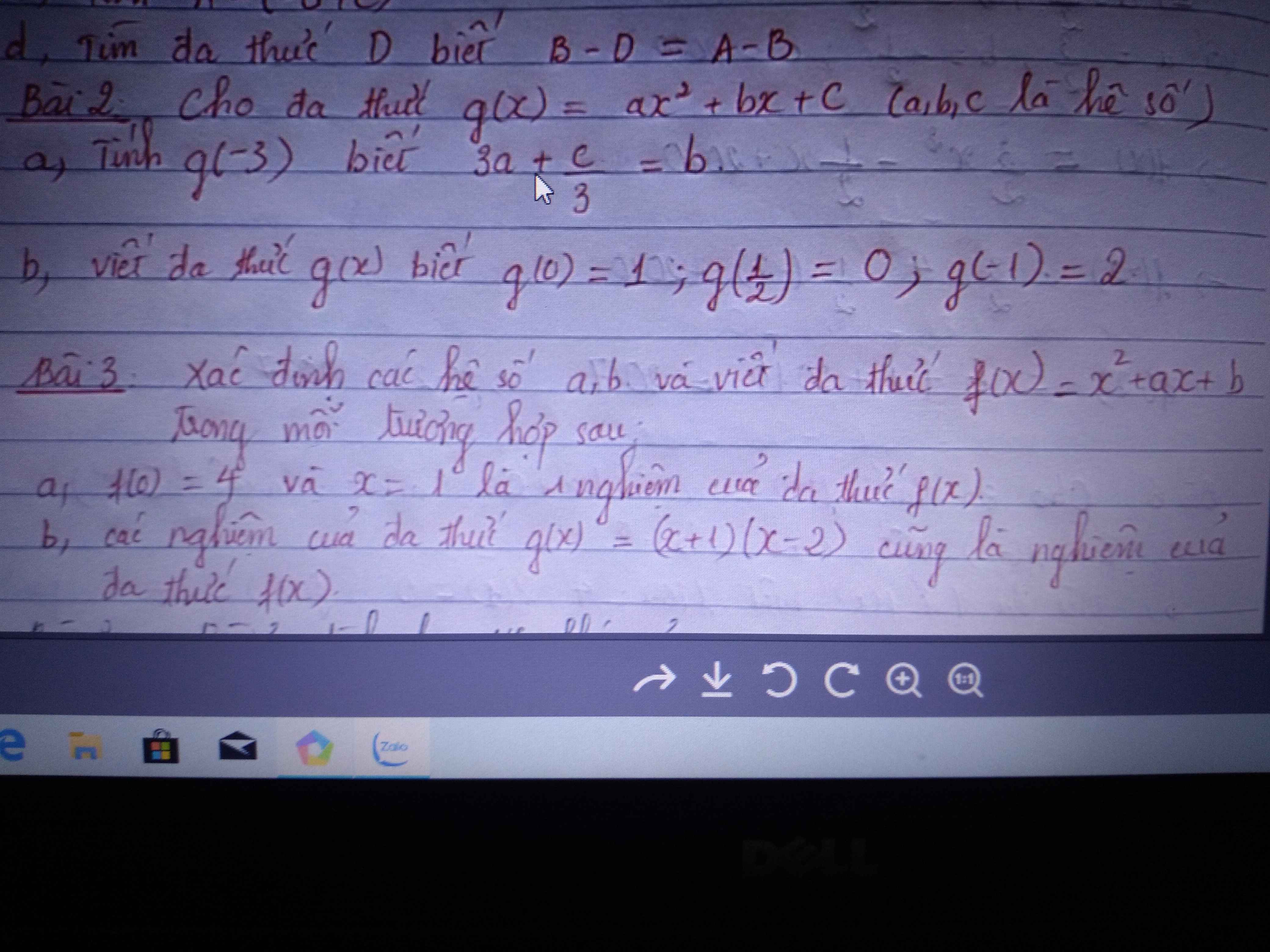
Bài 3:
a: Ta có: f(0)=4 và f(1)=0
\(\Leftrightarrow\left\{{}\begin{matrix}0^2-a\cdot0+b=4\\1^2+a\cdot1+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=4\\b+a=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=4\\a=-1-b=-5\end{matrix}\right.\)
b: Ta có: \(f\left(-1\right)=0\) và f(2)=0
\(\Leftrightarrow\left\{{}\begin{matrix}\left(-1\right)^2-a\cdot\left(-1\right)+b=0\\2^2-2a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b=-1\\-2a+b=-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3a=3\\a+b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-1-a=-2\end{matrix}\right.\)