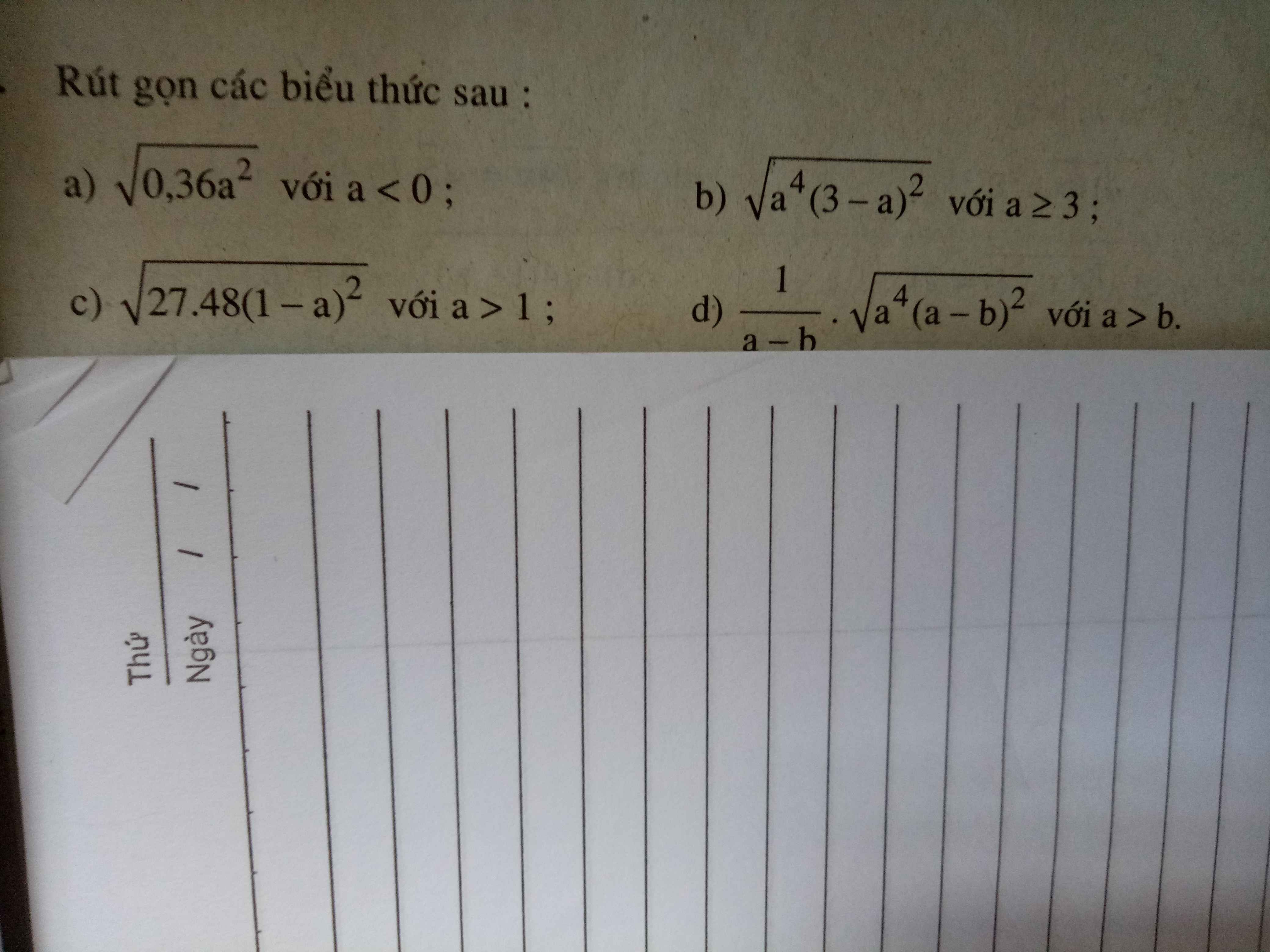a) \(\sqrt{0.36a^2}=0.6\left|a\right|=-\dfrac{3}{5}a\)
b) \(\sqrt{a^4\left(3-a\right)^2}=a^2\cdot\left|3-a\right|=a^2\left(a-3\right)=a^3-3a^2\)
c) \(\sqrt{27\cdot48\cdot\left(1-a\right)^2}=36\left|1-a\right|=36\left(a-1\right)=36a-36\)
d) \(\dfrac{1}{a-b}\cdot\sqrt{a^4\left(a-b\right)^2}=\dfrac{1}{a-b}\cdot a^2\cdot\left(a-b\right)=a^2\)
a)\(\sqrt{0,36a^2}=0,6\left|a\right|=-0,6a\)
b)\(\sqrt{a^4\left(3-a\right)^2}=\sqrt{a^4}\sqrt{\left(3-a\right)^2}=\left|a^2\right|.\left|3-a\right|\)
vì \(a\ge0\) nên \(\left|a^2\right|=a^2\)
vì \(a\ge3nên\left|3-a\right|=a-3\)
vậy \(\sqrt{a^4\left(3-a\right)^2}=a^2\left(a-3\right)\)
c)
\(\sqrt{27.48\left(1-a\right)^2}=\sqrt{27.3.6\left(1-a\right)^2}\\ =9.4\left|1-a\right|\)
vì a>1nên1-a<0d= do đó \(\left|1-a\right|=0-1\)
vậy \(\sqrt{27.48\left(1-a\right)^2}=36\left(a-1\right)\)
d)\(\dfrac{1}{a-b}:\sqrt{a^4\left(a-b\right)^2}=\dfrac{1}{a-b}:\left(\sqrt{10^4}\sqrt{\left(a-b\right)^2}\right)\)
\(=\dfrac{1}{a-b}:\left(a^2\left(a-b\right)\right)\)