\(V=\dfrac{1}{3}\pi r^2h=\dfrac{1}{3}\pi.2^2.3=4\pi\)
Chọn B
\(V=\dfrac{1}{3}\pi r^2h=\dfrac{1}{3}\pi.2^2.3=4\pi\)
Chọn B
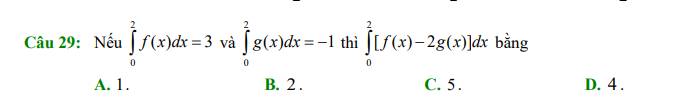
Giải giúp mình với ạ.
Câu 29 trong đề thi thử tốt nghiệp THPT môn Toán năm 2023 trường THPT Trần Phú, Đà Nẵng – CÓ ĐÁP ÁN: https://dethitoan.com.vn/de-thi-thu-tot-nghiep-thpt-mon-toan-nam-2023-truong-thpt-tran-phu-da-nang-co-dap-an/
hi hi Lớp học thực tế với chủ đề “Phát âm cơ bản” là chương trình học đem lại trải nghiệm là một thành viên thực sự trong lớp học. Với sự hướng dẫn rất sáng tạo và cuốn hút của thầy giáo Daniel đến từ Anh quốc sẽ giúp bạn phát âm theo đúng chuẩn quốc tế.
Tìm min f(x,y) = x+y với điều kiện (x-1)2 + y2 <=1 và x2 + y2 <=2
Các bạn giúp dùm mình với....
Đề số 1:
Bài tập 4: Trong không gian cho M (1 ; 2 ; 3) N (- 3 ; 4 ; 1).
P x + 2y - z + 4 = 0
a, Viết phương trình mặt phẳng trung trực MN
b, Viết phương trình mặt phẳng \(\left(\beta\right)\) đi qua MN và song song (P)
Trực giao hóa cơ sở sau
1 -1 1
1 0 1
1 2 0
Xin lỗi vì mik chưa biết cách viết bài toán
tìm x
\(\frac{1+3y}{12}=\frac{1+6y}{16}=\frac{1+9y}{4x}\)
Bài 1: Thực hiện phép tính. a) 136 – (2 . 52 + 23 . 3) b) (-243) + (-12) + (+243) + (-38) + (10)
Bài 2: Tìm x ∈ N, biết: a) 6 . (x – 81) = 54 b) 18 – (x – 4) = 32
Bài 3: Biết số học sinh của một trường trong khoảng từ 700 đến 800 học sinh, khi xếp hàng 30, hàng 36, hàng 40 đều vừa đủ hàng. Tính số học sinh của trường đó.
Bài 4: Cho đoạn thẳng CD = 6cm, lấy điểm M thuộc đoạn thẳng CD sao cho CM = 2cm.
a) Tính độ dài đoạn thẳng MD.
b) Trên tia đối của tia CM, lấy điểm N sao cho CN = 2cm. Chứng tỏ điểm C là trung điểm của đoạn thẳng NM.
các bạn giải giúp mình mấy câu bất đẳng thức này với
1) tìm GTLN
a) y=(6x+3)(5-2x) \(\dfrac{-1}{2}\le x\le\dfrac{5}{2}\)
b)y=\(\dfrac{x}{x^2+2}\) x>0
2)cho 3 số thực a,b,c thỏa mãn \(a\ge9,b\ge4,c\ge1\). CM :\(ab\sqrt{c-1}+bc\sqrt{a-9}+ca\sqrt{b-4}\le\dfrac{11abc}{12}\)
3)cho x,y>0 thỏa mãn x+y=2 . CM
a)xy(x2+y2)\(\le2\)
b)x3y3(x3+y3)\(\le2\)
4) x,y là các số thực thỏa mãn \(0\le x\le3,0\le y\le4\)
tìm GTLN A= (3-x)(4-y)(2x+3y)
5) biết x,y,z,u\(\ge0\)và 2x+xy+z+yzu=1
tìm GTLN của P=x2y2z2u
6)cho a,b,c>0 và a+b+c=3 .CMR:\(a\sqrt{b^3+1}+b\sqrt{c^3+1}+c\sqrt{a^3+1}\le5\)
7) cho 3 số dương x,y,z có tổng bằng 1 .CMR : \(\sqrt{\dfrac{xy}{xy+z}}+\sqrt{\dfrac{yz}{yz+x}}+\sqrt{\dfrac{xz}{xz+y}}\le\dfrac{3}{2}\)
8)cho 3 số dương a,b,c có tổng bằng 3 .
tìm GTLN của S=\(\dfrac{bc}{\sqrt{3a+bc}}+\dfrac{ca}{\sqrt{3b+ca}}+\dfrac{ab}{\sqrt{3c+ab}}\)
ko cần làm chi tiết lắm chỉ cần hướng dẫn là đc zùi