Ôn thi vào 10
Các câu hỏi tương tự
1, pt 3x2-5x-60 có tính 2 nghiệm bằng a, 2 b, -2 c, -6 d, dfrac{5}{3}2, biết widehat{ABx} là góc tạo bởi tiếp tuyến và dây cung chắn cung widehat{AmB} nếu widehat{ABx}120^o thì sđ widehat{AmB} bằng a, 60o b, 120o c, 240o d, 180o3, pt x2-6x-50 có tổng 2 nghiệm là S và tichs 2 nghiệm là P thìa, S-6; P5 b, S6; P5 ...
Đọc tiếp
1, pt 3x2-5x-6=0 có tính 2 nghiệm bằng
a, 2 b, -2 c, -6 d, \(\dfrac{5}{3}\)
2, biết \(\widehat{ABx}\) là góc tạo bởi tiếp tuyến và dây cung chắn cung \(\widehat{AmB}\) nếu \(\widehat{ABx}=120^o\) thì sđ \(\widehat{AmB}\) bằng
a, 60o b, 120o c, 240o d, 180o
3, pt x2-6x-5=0 có tổng 2 nghiệm là S và tichs 2 nghiệm là P thì
a, S=-6; P=5 b, S=6; P=5 c, S=6; P=-5 d, S=-5; P=6
4, hai số \(2+\sqrt{3}\) và \(2-\sqrt{3}\) là 2 nghiệm của pt nào sao đây
a, x2-4x-1=0 b, x2+4x-1=0 c, x2+4x+1=0 d, x2-4x+1=0
5, gọi x1; x2 là 2 nghiệm của pt 2x2+3x-5=0 biểu thức \(x_1^2+x_2^2\) có giá trị là
a, \(\dfrac{-3}{2}\) b, 26 c, \(\dfrac{29}{4}\) d, \(\dfrac{25}{4}\)
6, tất cả các giá trị của m để pt x2+2x+m-6=0 có 2 nghiệm trái dấu là
a, m≥6 b, m<6 c, m>6 d,≠6
7, cho tứ giác ABCD nội tiếp đg tròn tâm O đg kính CD hai đg chéo AC và BD cắt nhau tại K biết cung nhỏ AB có số đo bằng 60o khi đó \(\widehat{AKB}\) có số đo bằng
a, 60o b, 120o c, 240o d, 90o
8, đg thẳng y=2x+3 cắt parabol y=x2 tọa độ các gia điểm là
a, (-1;-1) và (3;9) b, (-1;1) và (3;9) c, (-1;1) và (3;6) d, (-1;-1) và (9;3)
9, tất cả các giá trị của k để pt x2+2x+k2-2k+2=0 có nghiệm là
a, k>1 b, k≠1 c, k=1 d, k\(\in\) R
10, từ điểm M ở ngoài đg tròn (O;R) vẽ tiếp tuyến MT và cắt tuyến MCD qua tâm O cho MT=10, MD=40 khi đó R bằng
a, 25 b, 20 c, 15 d, 30
Từ một điểm A nằm ngoài đường tròn tâm O bán kính R,kẻ các tiếp tuyến AB,AC với đường tròn (B,C là các tiếp điểm).Trên cung nhỏ Bc lấy một điểm M bất kì khác B và C.Gọi I , K , P lần lượt là hình chiếu vuông góc của điểm M trên các đoạn thẳng AB,AC,BC.
Chứng minh AIMK là tứ giác nội tiếp.
Cho (O) và dây BC cố định,không đi qua tâm.Điểm A thay đổi trên cung lớn BC(A khác B,C), điểm I là điểm chính giữa cung nhỏ BC. Gọi H, K lần lượt là hình chiếu vuông góc của I trên các đường thẳng AB, AC. Chứng minh:a) Bốn điểm A, H, I, K cùng thuộc một đường tròn.b) ΔIHK là Δ cân và Góc HIK Góc BIC.c) Khi A thay đổi trên cung lớn BC thì đường thẳng HK luôn đi qua một điểm cố định.
Đọc tiếp
Cho (O) và dây BC cố định,không đi qua tâm.Điểm A thay đổi trên cung lớn BC(A khác B,C), điểm I là điểm chính giữa cung nhỏ BC. Gọi H, K lần lượt là hình chiếu vuông góc của I trên các đường thẳng AB, AC. Chứng minh:
a) Bốn điểm A, H, I, K cùng thuộc một đường tròn.
b) ΔIHK là Δ cân và Góc HIK = Góc BIC.
c) Khi A thay đổi trên cung lớn BC thì đường thẳng HK luôn đi qua một điểm cố định.
Cho (O;R), dây cung BC( khác đg kính). Điểm A di động trên cung lớn BC(A khác B,C). Kẻ đg kính AD của (O), H là chân đg vuông góc kẻ từ A đến BC. Hai đ E,F lần lượt là chân đuong vuông góc kẻ từ B,C đến AD.CMR:
1.A,B,H,E cùng thuộc 1 đường tròn
2.R=(AB.AC):(2AH)
3.HE vuông góc AC và tâm đg tròn ngoại tiếp tam giác HEF là 1 điểm cố định
Cho đường tròn tâm O bán kính r dây AB=R căn 3 và K là điểm chính giữa cung lớn AB.Gọi M là điểm tùy ý trên cung nhỏ BK(M khác B;K).Trên tia AM lấy điểm N sao cho AN=BM.Kẻ BP//KM(P thuộc tâm O) a) Chứng minh ANKP là hình bình hành
Từ điểm M cố định nằm ngoài đường tròn (O) vẽ hai tiếp tuyến MA, MB (A và B
là hai tiếp điểm). Điểm I thuộc cung nhỏ AB (I khác A và B). Tiếp tuyến tại I của đường
tròn (O) cắt MA, MB lần lượt ở E và K.
a) Chứng minh: chu vi tam giác MEK có giá trị không đổi khi I di
động trên cung nhỏ AB.
Cho AB là 1 dây cung khác đường kính của đường tròn (O). Điểm C thay đổi trên cung lớn AB. Gọi A', B' là hình chiếu vuông góc của A,B xuống phân giác góc ACB. Chứng minh rằng A',B' thuộc những đường tròn cố định.
Giúp mk nhanh nháaaa
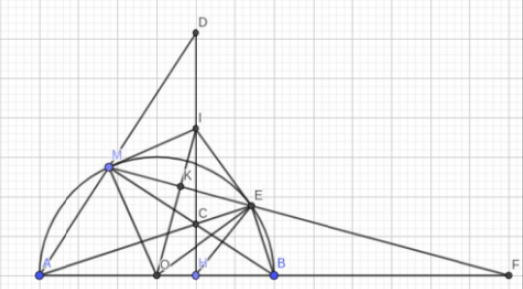
Từ một điểm A nằm ngoài đường tròn tâm O, bán kính R (AO 2R) vẽ hai tiếp tuyến AD, AE với (O) (D,E là các tiếp điểm).Gọi H là giao điểm của DE và AO.Lấy điểm M thuộc cung nhỏ DE (M khác D khác E, MD ME).Tia AM cắt đường tròn (O;R) tại N.Đoạn thẳng AO cắt cung nhỏ DE tại K.a) Chứng minh AO vuông góc với DE và AD2 AM.ANb) Chứng minh NK là tia phân giác của góc DNI và tứ giác MHON nội tiếp.c) Kẻ đường kính KQ của đường tròn (O;R).Tia QN cắt tia ED tại C.Chứng minh MD.CE ME.CD
Đọc tiếp
Từ một điểm A nằm ngoài đường tròn tâm O, bán kính R (AO < 2R) vẽ hai tiếp tuyến AD, AE với (O) (D,E là các tiếp điểm).Gọi H là giao điểm của DE và AO.Lấy điểm M thuộc cung nhỏ DE (M khác D khác E, MD < ME).Tia AM cắt đường tròn (O;R) tại N.Đoạn thẳng AO cắt cung nhỏ DE tại K.
a) Chứng minh AO vuông góc với DE và AD2 = AM.AN
b) Chứng minh NK là tia phân giác của góc DNI và tứ giác MHON nội tiếp.
c) Kẻ đường kính KQ của đường tròn (O;R).Tia QN cắt tia ED tại C.Chứng minh MD.CE = ME.CD
8/75cho đường tròn O đường kính AB , điểm C nằm trên đường tròn (C khác A và B) . gọi M,N lần lượt là điểm chính giữa của cung AC nhỏ và cung BC nhỏ . gọi E là giao điểm của ON và CB . từ N vẽ NK vuông góc AC ( K thuộc AC)A/ chứng minh tứ giác ECKN là hình chữ nhật và suy ra KN là tiếp tuyến tại N của đường tròn OB/ vẽ đường kinh ND của đường tròn O . chứng minh tứ giác KEDA là hình bình hànhC/ gọi I là giao điểm của MN và KO . chứng minh (căn 2) /NI 1/NK + 1/NOthankkkkkkkkkkkkkkkkkkkk
Đọc tiếp
8/75
cho đường tròn O đường kính AB , điểm C nằm trên đường tròn (C khác A và B) . gọi M,N lần lượt là điểm chính giữa của cung AC nhỏ và cung BC nhỏ . gọi E là giao điểm của ON và CB . từ N vẽ NK vuông góc AC ( K thuộc AC)
A/ chứng minh tứ giác ECKN là hình chữ nhật và suy ra KN là tiếp tuyến tại N của đường tròn O
B/ vẽ đường kinh ND của đường tròn O . chứng minh tứ giác KEDA là hình bình hành
C/ gọi I là giao điểm của MN và KO . chứng minh (căn 2) /NI = 1/NK + 1/NO
thankkkkkkkkkkkkkkkkkkkk