Ta có hình vẽ:
Giải:
Xét \(\Delta ACD\) có \(\widehat{D}=90^o\) vì \(ABCD\) là hình chữ nhật.
\(\Rightarrow A^2=AD^2+DC^2\) ( theo định lí Pitago)
Mà \(DC=36cm;AD=48cm\)
Nên \(AC^2=48^2+36^2\)
\(AC^2=2304+1296\)
\(AC^2=3600\)
\(\Rightarrow AC=60cm\)
Vậy độ dài của đoạn \(AC\) là \(60cm\)
Bài 59. Bạn Tâm muốn đóng cho một nẹp chéo AC để khung hình chữ nhật ABCD được vững hơn(h.134). Tính độ dài AC, Biết rằng AD=48 cm, CD=36 cm.
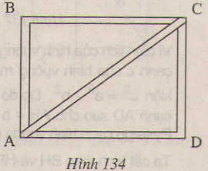
Giải:
Theo định lí Pytago, ta có:
AC2= AD2 +CD2
= 482 + 362
= 2304 + 1296= 3600
AC= 60 (cm)
Ta có : ABCD là hình chữ nhật
=> ADC = 90o
=> tam giác ADC vuông tại D
=> AC2 =AD2 + CD2 ( ĐL Pi-ta-go )
<=> AC2 = 482 =362 =3600
<=> AC = \(\sqrt{3600}\)
<=> 60 (cm)
Vậy AC = 60 (cm)













