Question

 

Bài 8. Cho hình thang ABCD (AB// CD). Hai đường phân giác của góc D và C giao nhau tại K nằm trên AB. Chứng minh AB= AD+ BC.

mik cần gấp ạ 

 

Answer 1

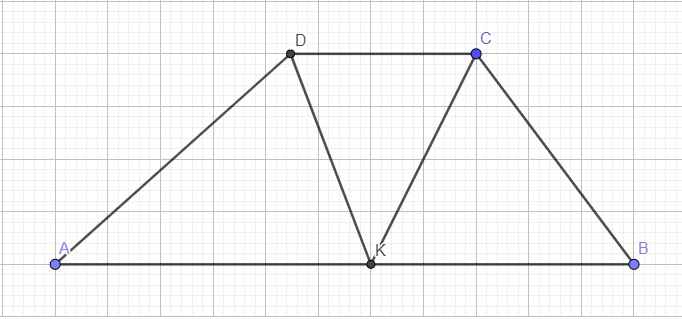
Ta có:

\(AB||CD\Rightarrow\widehat{AKD}=\widehat{CDK}\) (so le trong)

Mà \(\widehat{CDK}=\widehat{ADK}\) (do DK là phân giác góc D)

\(\Rightarrow\widehat{ADK}=\widehat{AKD}\)

\(\Rightarrow\Delta ADK\) cân tại A

\(\Rightarrow AD=AK\) (1)

Tương tự ta có: \(\widehat{DCK}=\widehat{BKC}\) (so le trong)

\(\widehat{DCK}=\widehat{BCK}\) (CK là phân giác góc C)

\(\Rightarrow\widehat{BCK}=\widehat{BKC}\Rightarrow\Delta BCK\) cân tại B

\(\Rightarrow BC=BK\) (2)

(1);(2) \(\Rightarrow AB=AK+BK=AD+BC\) (đpcm)

Answer 2