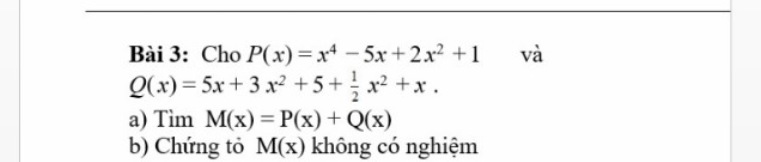Question

Bài 7b mn ơi

Answer 1

mờ quá bạn ah

 

Answer 2

có: x⁴≥0

    x²≥0  =>2x²≥0

=>x⁴ + 2x² ≥0

=>x⁴ + 2x² + 5 >0

=> x⁴ + 2x² + 5 vô nghiệm

hay M(x) vô nghiệm

Answer 3

c.N(x)=x^2−2x+5x2−2x+5

=x^2−x−x+1+4=x^2−x−x+1+4

=(x^2−x)−(x−1)+4=(x^2−x)−(x−1)+4

=x(x−1)−(x−1)+4=x(x−1)−(x−1)+4

=(x−1)(x−1)+4=(x−1)(x−1)+4

=(x−1)2+4>0+4>0=(x−1)2+4>0+4>0

Vậy: Đa thức trên vô nghiệm

Answer 4

M(x) = x⁴ + 2x² + 5

Đặt M(x) = 0 

Tức là x⁴ + 2x² + 5 = 0

x⁴ ≥ 0 với mọi giá trị x 

2x²  ≥ với mọi giá trị x 

mà 5 > 0

x⁴ + 2x² + 5 > 0

=> Đa thức trên vô nghiệm