Ôn tập chương II - Đa giác. Diện tích đa giác
Các câu hỏi tương tự
Cho hình chữ nhật ABCD. Gọi H, I, E, K lần lượt là các trung điểm của BC, HC, DC, EC (h.159)
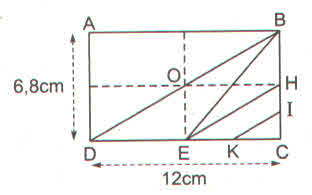
Tính :
a) Diện tích tam giác DBE
b) Diện tích tứ giác EHIK
Cho tứ giác ABCD. Hai đường chéo AC và BD vuông góc với nhau. Gọi E, F, G và H lần lượt là trung điểm của các cạnh AB, BC, CD và DA
a) chứng minh tứ giác EFGH là hình chữ nhật
b) biết AC=10cm, BD=8cm. Tính diện tích tứ giác EFGH
c) Để EFGH là hình vuông thì tứ giác ABCD cần có thêm điều kiện gì về hai đường chéo ?
Cho hình thang ABCD (AB//CD); E là trung điểm của AD. Gọi H là hình chiếu của E trên đường thẳng CD. Qua E, vẽ đường thẳng song song với BC, cắt đường thẳng AB và CD lần lượt tại I và K. Cho biết EH = 5 cm, BC = 8 cm; tính diện tích tứ giác IBCK, ABC...
Cho tam giác ABC cân tại A , đường cao AH . Biết AB 5cm; BC 6cm. a) Tính diện tích ∆ABC . b) Gọi M là trung điểm của AB ; Q là điểm đối xứng với H qua M . Tứ giác AHBQ là hình gì? Vì sao? c) Gọi F là điểm đối xứng với A qua BC ; N là giao điểm của QF và BH . Tính độ dài đoạn thẳng MN . d) Vẽ HK vuông góc với CF tại K ; ∆ABC cần thêm điều kiện gì để ba điểm Q , H , K thẳng hàng? e) Gọi I là trung điểm của HK . Chứng minh FI vuông góc với BK
Đọc tiếp
Cho tam giác ABC cân tại A , đường cao AH . Biết AB = 5cm; BC = 6cm. a) Tính diện tích ∆ABC . b) Gọi M là trung điểm của AB ; Q là điểm đối xứng với H qua M . Tứ giác AHBQ là hình gì? Vì sao? c) Gọi F là điểm đối xứng với A qua BC ; N là giao điểm của QF và BH . Tính độ dài đoạn thẳng MN . d) Vẽ HK vuông góc với CF tại K ; ∆ABC cần thêm điều kiện gì để ba điểm Q , H , K thẳng hàng? e) Gọi I là trung điểm của HK . Chứng minh FI vuông góc với BK
cho tam giác DEF cân tại D có đường cao DH gọi M là trung điểm của D và N là điểm đối xứng của H qua m A. biết DH = 4 cm BC = 14 cm tính diện tích tam giác DHE. B tứ giác DHFN là hình gì ? vì sao?
Cho tam giác ABC. Gọi M, N là các trung điểm tương ứng của AC, BC. Chứng minh rằng diện tích của hình thang ABNM bằng \(\dfrac{3}{4}\) diện tích của tam giác ABC ?
Cho hình chữ nhật ABCD( AB>BC). Từ B kẻ BH vuông góc với AC tại H. Lấy E sao cho H là trung điểm BE, lấy Q đối xứng với C qua H.
a) Tứ giác BCEQ là hình gì? Vì sao?
b)QE cắt DC tại M. Gọi N là hình chiếu của E trên AD, MN cắt DE tại o.CM tam giác OEM là tam giác cân
c) chứng minh rằng ADCE là hình thang cân
d) chứng minh 3 điểm N, M, H thẳng hàng
Cho hình bình hành ABCD. Gọi K và L là hai điểm thuộc cạnh BC sao cho BK = KL = LC. Tính tỉ số diện tích của
a) Các tam giác DAC và DCK
b) Tam giác DAC và tứ giác ADLB
c) Các tứ giác ABKD và ABLD
Cho tam giác MNP vuông tại N. Biết MN=6cm,NP=8cm, đường cao NH. Qua H kẻ HC⊥MN,HD⊥NP
a)Chứng minh tứ giác HDNC là hình chữ nhật
b)chứng minh NH.MP=MN.NP
c)tính độ dài CD
d)tính diện tích tam giác NMH








