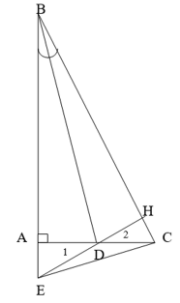
a). Xét t/g : ABD và HBD có:
góc A = góc H = 90\(^o\)
BD cạnh chung
góc ABD = góc HBD ( BD là tia ph/giác góc B)
do đó :
t/g ABD = t/g HBD ( cạnh huyền - góc nhọn).
b, Vì t/g ABD = t/g HBD
=> AD = HD và AB=HB (1) ( 2 cạnh tương ứng).
Xét t/g ADE và HDC có:
góc A = góc H = 90\(^o\)
góc D1 = góc D2 ( đối đỉnh).
AD = HD ( cmt)
do đó : t/g ADE = t/g HDC ( cạnh góc vuông - góc nhọn kề nó).
=> AE = HC ( 2) ( 2 cạnh tương ứng).
Từ (1) và (2) suy ra : AB + AE = HB + HC
Hay BE = BC
=> T/g BEC cân tại B.
c).
Theo cmt ta có AD = DH
Xét t/g vuông DHC vuông tại H có:
DH<DC
Do đó:
AD < DC













