a/ \(\frac{1-cos\left(2x+\frac{\pi}{2}\right)-1}{cosx\left(\frac{1}{sinx}-sinx\right)}=\frac{sin2x}{cosx\left(\frac{1-sin^2x}{sinx}\right)}=\frac{2sinx.cosx.sinx}{cosx.cos^2x}=\frac{2sin^2x}{cos^2x}=2tan^2x\)
b/ \(x^2+2x+2019=\left(x+1\right)^2+2018>0\) \(\forall x\)
\(-1\le\frac{x^2-2x-m}{x^2+2x+2019}\Leftrightarrow x^2-2x-m\ge-x^2-2x-2019\)
\(\Leftrightarrow2x^2\ge m-2019\) \(\forall x\)
\(\Rightarrow m-2019\le0\Rightarrow m\le2019\)
\(\frac{x^2-2x-m}{x^2+2x+2019}< 2\Leftrightarrow x^2-2x-m< 2x^2+4x+4038\)
\(\Leftrightarrow x^2-6x+9>-m-4029\)
\(\Leftrightarrow\left(x-3\right)^2>-m-4029\) \(\forall x\)
\(\Rightarrow-m-4029< 0\Rightarrow m>-4029\)
Vậy \(-4029< m\le2019\)







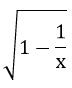 là:
là: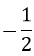 x + y = -1 B.
x + y = -1 B. 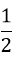 x - y = -1
x - y = -1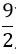 ) D.(2; 2) và (-3;
) D.(2; 2) và (-3; 


