Đặt A = 2n + 1 (*)
+) Với n = 1 ta có A = 3 chia hết cho 3
+) Với n > 1 giả sử (*) đúng với n = 2k + 1( k thuộc N ) => 22k+1 + 1 chia hết cho 3
Cần chứng minh (*) đúng với n = 2k + 3
Ta có : A = 2n + 1 = 22k+3 + 1 = 22k+1+2 + 1 = 22k+1.22 + 1
= 4( 22k+1 - 2 ) + 9 = 4( 22k+1 + 1 - 3 ) + 9 = 4.(22k+1 + 1 ) - 3 chia hết cho 3 ( theo giả thiết quy nạp )
Vậy ta có đpcm
Bài giải này nếu có sai sót mong các bạn/anh/chị sửa ạ:v
\(n=2k+1\Rightarrow A=2^n+1=2^{2k+1}+1=2.4^k+1\)
Do \(4\equiv1\left(mod3\right)\Rightarrow4^k\equiv1\left(mod3\right)\Rightarrow2.4^k\equiv2\left(mod3\right)\)
\(\Rightarrow2.4^k+1\equiv3\left(mod3\right)\) hay \(2.4^k+1⋮3\Rightarrow A⋮3\)










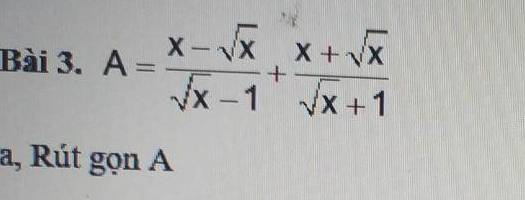

 ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn
ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn 






