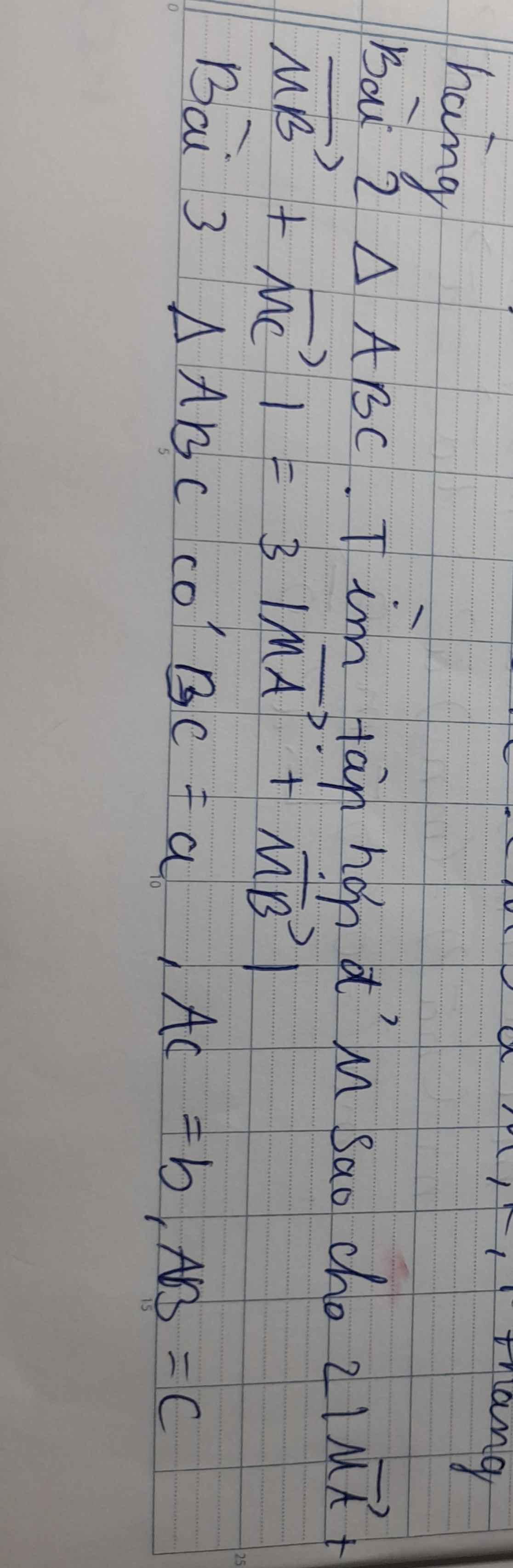a) Các vecto khác \(\overrightarrow{0}\) và cùng phương vơi vecto \(\overrightarrow{AI}\)là:
\(\overrightarrow{IM},\overrightarrow{AM}\)
b) Chứng minh: \(\overrightarrow{IB}+\overrightarrow{IC}+2\overrightarrow{IA}=0\)
Có \(\overrightarrow{IB}=\overrightarrow{MB}-\overrightarrow{MI}\)
\(\overrightarrow{IC}=\overrightarrow{MC}-\overrightarrow{MI}\)
\(\Rightarrow\overrightarrow{IB}+\overrightarrow{IC}=-2\overrightarrow{MI}\) (do \(\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\) do M là trung điểm AB).
Mặt khác: \(\overrightarrow{MI}=\overrightarrow{IA}\)
\(\Rightarrow-2\overrightarrow{MI}+2\overrightarrow{IA}=0\)
Vậy \(\overrightarrow{IB}+\overrightarrow{IC}+2\overrightarrow{IA}=0\)