\(f\left(x_1\right)-f\left(x_2\right)=3x_1-3x_2=3\left(x_1-x_2\right)< 0\)
=>\(f\left(x_1\right)< f\left(x_2\right)\)
=>Hàm số đồng biến trên R
Đúng 0
Bình luận (3)
Bài 1: Nhắc lại và bổ sung các khái niệm về hàm số
Các câu hỏi tương tự
Cho hàm số \(y=f\left(x\right)=3x\)
Cho \(x\) hai giá trị bất kì \(x_1,x_2\) sao cho \(x_1< x_2\)
Hãy chứng minh \(f\left(x_1\right)< f\left(x_2\right)\) rồi rút ra kết luận hàm số đã cho đồng biến trên \(\mathbb{R}\)
Cho hàm số y=f(x)=2x-3. X lấy giá trị thực bất kì x1, x2 sao cho x1 < x2. Chứng tỏ f(x1) < f(x2). Kết luận về tính biến thiên của hàm số
a) Cho hàm số :
yfleft(xright)dfrac{2}{3}x
Tính :
fleft(-2right);fleft(-1right);fleft(0right);fleft(dfrac{1}{2}right);fleft(1right);fleft(2right)
b) Cho hàm số :
ygleft(xright)dfrac{2}{3}x+3
Tính :
gleft(-2right);gleft(-1right);gleft(0right);gleft(dfrac{1}{2}right);gleft(1right);gleft(2right)
c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến x lấy cùng một giá trị ?
Đọc tiếp
a) Cho hàm số :
\(y=f\left(x\right)=\dfrac{2}{3}x\)
Tính :
\(f\left(-2\right);f\left(-1\right);f\left(0\right);f\left(\dfrac{1}{2}\right);f\left(1\right);f\left(2\right)\)
b) Cho hàm số :
\(y=g\left(x\right)=\dfrac{2}{3}x+3\)
Tính :
\(g\left(-2\right);g\left(-1\right);g\left(0\right);g\left(\dfrac{1}{2}\right);g\left(1\right);g\left(2\right)\)
c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến x lấy cùng một giá trị ?
Cho hàm số \(y=f\left(x\right)=4-\dfrac{2}{5}x\) với \(x\in\mathbb{R}\)
Chứng minh rằng hàm số đã cho nghịch biến trên \(\mathbb{R}\)
Cho hàm số \(y=f\left(x\right)=\dfrac{2}{3}x+5\) với \(x\in\mathbb{R}\)
Chứng minh rằng hàm số đồng biến trên \(\mathbb{R}\)
Cho hàm số \(y=f\left(x\right)=1,2x\). Tính các giá trị tương ứng của y khi cho x các giá trị sau đây, rồi lập bảng giá trị tương ứng giữa x và y :
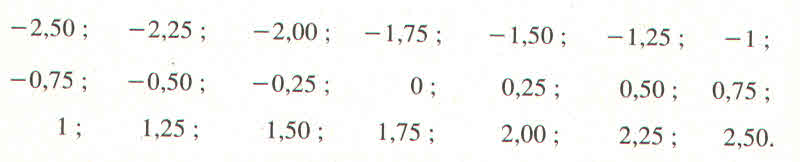
Cho hàm số y=f(x)=x mũ 2. Xét tính biến thiên của hàm số trong khoảng từ (0;1) và 1>x1>x2>0
Cho hàm số f(x)=\(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
a) tìm tập xác định của hàm số
b) tính \(f\left(4-2\sqrt{3}\right)\)và \(f\left(a^2\right)\) với a<-1
c) tìm x nguyên để f(x) là số nguyên
d) Tìm x sao cho f(x)=f\(\left(x^2\right)\)
Tìm giá trị nhỏ nhất
\(A=\left|x_1^2-x_2^2\right|\\\left|x_1-x_2\right| \left|x_1+x_2\right|\\ 4\left|x_1^{ }-x_2^{ }\right|\)
Mình không hiểu tại sao là \(4\left|x_1^{ }-x_2^{ }\right|\)