Ôn tập: Tam giác đồng dạng
Các câu hỏi tương tự
Cho tam giác ABC cân tại đỉnh A , có đường cao AH. Gọi M là 1 điểm di động trên cạnh BC. Điểm D và E lần lượt thuộc cạnh AB và AC sao cho tứ giác ADME là hình bình hành. Gọi I là giao điểm của BE và CD.a) Chứng minh rằng : widehat{DMI}widehat{AME}b) Chứng minh rằng đường thẳng MI luôn luôn đi qua 1 điểm cố định .P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán giúp đỡ, em cám ơn nhiều lắm ạ!
Đọc tiếp
Cho tam giác ABC cân tại đỉnh A , có đường cao AH. Gọi M là 1 điểm di động trên cạnh BC. Điểm D và E lần lượt thuộc cạnh AB và AC sao cho tứ giác ADME là hình bình hành. Gọi I là giao điểm của BE và CD.
a) Chứng minh rằng : \(\widehat{DMI}=\widehat{AME}\)
b) Chứng minh rằng đường thẳng MI luôn luôn đi qua 1 điểm cố định .
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán giúp đỡ, em cám ơn nhiều lắm ạ!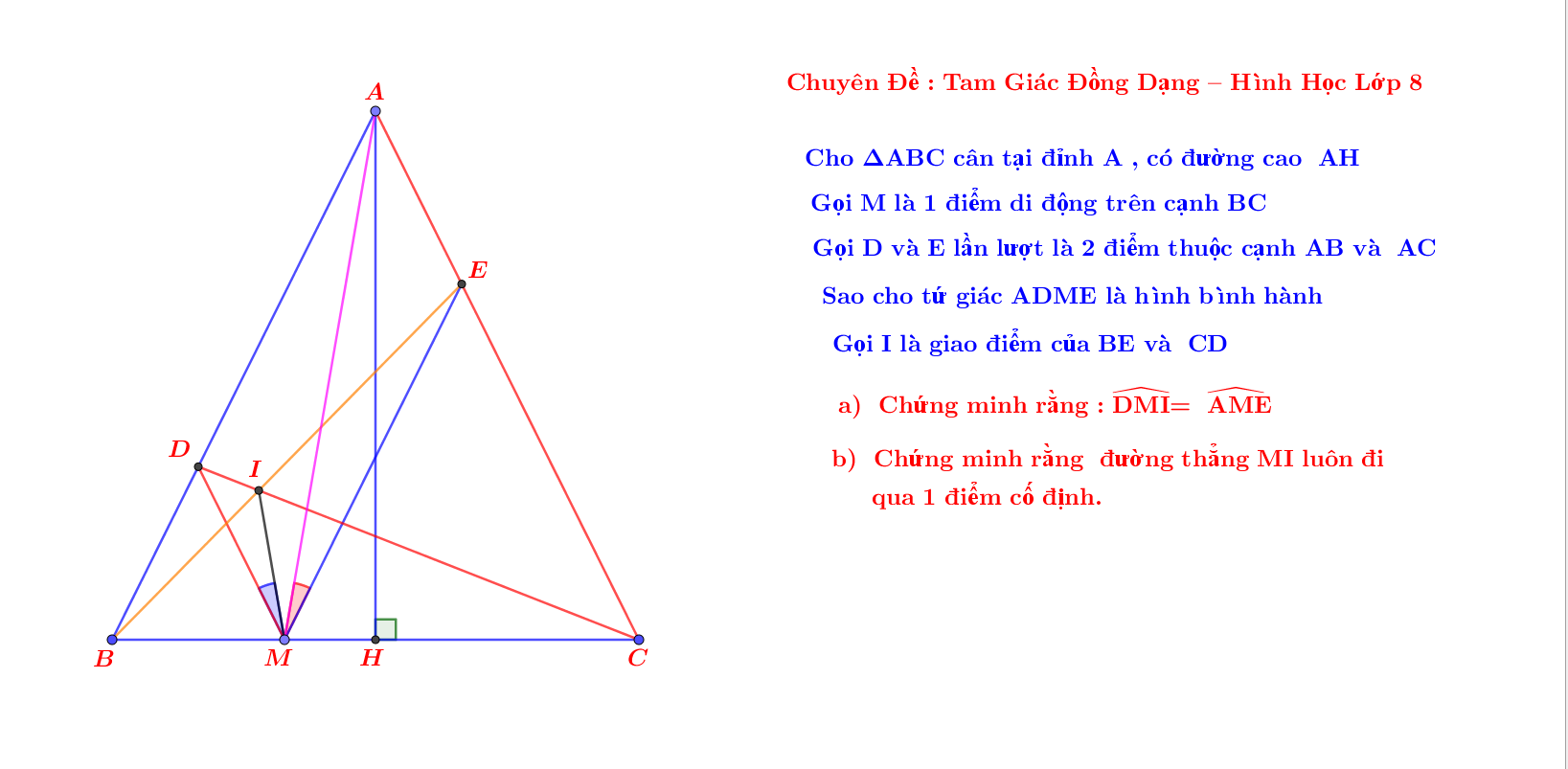
Cho tam giác ABC vuông tại A (AB>AC). Kẻ đường cao AH (H thuộc BC). Gọi D là trung điểm của AB. Qua A kẻ đường thẳng vuông góc với CD cắt CD và CB lần lượt tại E và F. Gọi K là hình chiếu vuông góc của D trên BC.
1) Chứng minh rằng các tam giác ADE và CDA đồng dạng với nhau.
2) Chứng minh rằng BD.BC = BE.CD.
Cho tam giác ABC vuông tại A và có đường cao AH.
a/ Chứng minh AHC đồng dạng với BAC và suy ra AH.BC=AB. AC
b/ Gọi CD là đường phân giác của góc ACB (D thuộc cạnh AB). CD cắt AH tại E. Chứng minh rằng: tam giác ACE đồng dạng với tam giác BCD.
c/ Gọi I là trung điểm của đoạn thẳng DE. Chứng minh rằng: AI vuông góc DE
Cho hình vuông ABCD có AB = a, hai đường chéo cắt nhau tại O. Trên hai cạnh AB, BC lần lượt lấy hai điểm E và G sao cho AE= BG. Gọi H là giao điểm của tia AG và tia DC, I là giao điểm của tia OG và đoạn thẳng BH.
1) Chứng minh rằng: AOGE là tam giác vuông cân.
Bài 3: Cho tam giác ABC vuông tại A (AC>AB), M là điểm trên cạnh AC. Vẽ MD vuông góc với BC tại D. Gọi E là giao điểm của hai đường thẳng MD và AB. a) Chứng minh: ∆CDM∾∆CAB. b) Chứng minh: MD.ME=MA.MC c) Chứng minh: 𝑀𝐴𝐷 ̂ = 𝑀𝐸𝐶 ̂ d) giả sử 𝑆𝐴𝐵𝐷𝑀 = 3𝑆𝐶𝐷𝑀, chứng minh: BC=2MC
Cho tam giác ABC một đường thẳng song song với cạnh BC cắt AB tại D và AC tại E. Trên tia đối của tia CA lấy điểm F sao cho CF=BD. Gọi M là giao điểm của DF và BC Chứng minh rằng: MD/MF = AC/AB. Cho BC=8cm, BD=5cm, DE=3cm . Chứng minh tam giác ABC cân
Mik đang cần gấp!!!
Cho tam giác ABC vuông tại A, có AB=6cm;BC=10cm và đường phân giác BD ( D thuộc cạnh AC). Kẻ DH vuông góc với BC ( H thuộc cạnh BC). a,Tính tỉ số AD/CD b,Nêu 2 cặp cạnh tam giác đồng dạng trên hình? c, Chứng minh AB.DC= HB.BC?
ho tam giác vuông abc vuông tại a có ab=6cm,ac=8cm. kẻ đường cao ah.
a) chứng minh tam giác abc đồng dạng với tam giác hba
b)tính độ dài các cạnh bc, ah,bh
c)gọi i và k lần lượt là hình chiếu của h lên cạnh ab và ac. Chứng minh ai.ab=ak.ac
Cho ∆ABC vuông tại A có đường cao AD gọi E,F lần lượt là hình chiếu vuông góc của D lên cạnh AB,AC a) chứng minh tam giác ∆BDA ~ ∆BAC b)Chứng minh AE . AB = AF . AC c) Chứng minh: EF³= BE.CF.BC










