Chứng minh:
Các điểm được đặt tên như hình vẽ:
Ta có:
Cơ mà
Lại có:
Đúng 0
Bình luận (0)
Ôn tập cuối năm phần hình học
Các câu hỏi tương tự
Cho ntam giác ABC trực tâm H . O là giao của ba đường trung trực ( 0 là tâm đường tròn ngọai tiếp tam gáic ABC) M là trung điểm ( MB=MC) Chứng minh rằng :
a/ AH//OM
b/ AH=2OM
c/ Chứng minh H,G,O thẳng hàng với G là trọng tâm tam giác ABC
29 tháng 4 2021 lúc 22:36
Cho tam giác ABC nhọn, các đường cao BE, CF cắt nhau tại H( E thuộc AC, F thuộc AB). Gọi O là giao điểm 3 đường trung trực của tam giác ABC. Chứng minh rằng khoảng cách từ O đến cạnh BC bằng một nửa độ dài AH
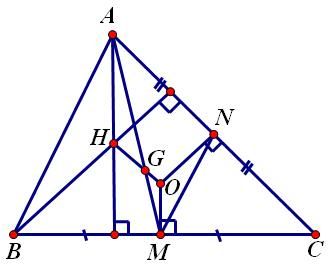
Cho tam giác ABC. Gọi M là trung điểm của BC, N là trung điểm AC. Các đường trung trực của BC và AC cắt nhau tại O. H là trực tâm, G là trọng tâm. Chứng minh:
a)Tam giác ABH đồng dạng với MNO
b)AHG đồng dạng với MOG
c)Ba điểm H,G,O thẳng hàng
Cho tam giác ABC trọng tâm G trực tâm H đường tròn ngọai tiếp O . Chứng minh rằng G , H < O thẳng hàng
cho tam giác ABc có trực tâm AH. Gọi M và N lần lượt là trung điểm của BC và AC. Gọi O là giao điểm của các đường trung trực của tam giác và G là trọng tâm của tam giác. Chứng minh:
a) \(\Delta OMN\sim\Delta HAB\Rightarrow AH=2OM\)
b) \(\Delta HAG\sim\Delta OMG\)
c) H, G, O thẳng hàng, GH = 2.GO
Cho tam giác ABC nhọn đường cao BD và CE cắt nhau taị H. I là trung điểm BC gọi K là điểm sao cho I là trung điểm KH , M là điểm sao cho BC là đường trung trực của MH 1. Tứ giác BCHKvaf BCMK là hình gì 2. O là trung điểm AK chứng monh O là giao điểm 3 đườn trung trực của tam gáic ABC 3. Chứng minh AK vuông góc với DE
cho tam giác ABC, có trực tâm H. Gọi M,N theo thứ tự là trung điểm của BC, AC. Gọi O là giao điểm các đường trung trực của tam giác
a, CM: ΔOMN∼ΔHBA. Tìm tỉ số đồng dạng
b, So sáng độ dài AH và OM
c, Gọi G là trực tâm của tam giác ABC. CM: ΔHAG∼ΔOMG
d, CM: H,G,O thẳng hàng và GH=2GO
4 tháng 1 2021 lúc 20:46
Cho tam giác ABC, H là trực tâm. Gọi M, N, P lần lượt là trung điểm AB, BC, CA. D, E, F lần lượt là trung điểm HA, HB, HC.
a, CM MNFD, MEFP là hình chữ nhật.
b, Tìm điều kiện để MD=ME=DP.
5 tháng 9 2021 lúc 20:06
Cho \(\Delta\)ABC nhọn, trực tâm H. Gọi M là trung điểm BC, K là trung điểm đối xứng H qua M.
a, Tứ giác BHCK là hình gì? Vì sao?
b, CM \(\Delta\)ACK vuông.
c, \(\Delta\)ABC cần có thêm điều kiện gì để tứ giác BHCK là hình thoi?