Chương 1:ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Các câu hỏi tương tự
Có bao nhiêu số nguyên m thuộc [-20;20] để đồ thị hàm số y=mx^4+(m^2-9)x^2+1 có ba điểm cực trị?
A. 20. B. 19. C. 18. D. 17.
\(\frac{5x-13-\sqrt{57+10x-3x^2 }} { \sqrt{x+3}- \sqrt{19-3x}} \ge x^2+2x+9\) giúp mình câu này với ạ
Câu 1 : Có bao nhiêu giá trị nguyên m để đồ thị hàm số yx^3-2m^2x^{2^{ }}-mx-1 đạt cực tiểu tại điểm x 1 ?
A. Vô số B. 2 C. 1 D. 0
Câu 2 : Tìm điều kiện m để đồ thị hàm số yfrac{x-1}{x^2-4x+m} có hai đường tiệm cận đứng
A. m 2 B. mle4 và mne3 C. m 4 và mne3 D. m 4
Câu 3 : Tìm giá trị lớn nhất M của hàm số yfrac{x^2+3}{x-1} trên đoạn [2;4]
A. M 7 B. M 6 C. M 19/3...
Đọc tiếp
Câu 1 : Có bao nhiêu giá trị nguyên m để đồ thị hàm số \(y=x^3-2m^2x^{2^{ }}-mx-1\) đạt cực tiểu tại điểm x = 1 ?
A. Vô số B. 2 C. 1 D. 0
Câu 2 : Tìm điều kiện m để đồ thị hàm số \(y=\frac{x-1}{x^2-4x+m}\) có hai đường tiệm cận đứng
A. m < 2 B. \(m\le4\) và \(m\ne3\) C. m < 4 và \(m\ne3\) D. m < 4
Câu 3 : Tìm giá trị lớn nhất M của hàm số \(y=\frac{x^2+3}{x-1}\) trên đoạn [2;4]
A. M = 7 B. M = 6 C. M = 19/3 D. M = 8
Câu 4 : Tìm giá trị cực tiểu của hàm số \(y=x^4-2x^2-5\)
A. \(y_{CT}=0\) B. \(y_{CT}=-6\) C. \(y_{CT}=\pm1\) D. \(y_{CT}=-5\)
Câu 5 : Tìm giá trị lớn nhất M của hàm số \(y=x^4-4x^2-2\) trên đoạn \(\left[0;\sqrt{3}\right]\)
A. M = -7 B. M = -6 C. M = -5 D. M = -2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác vuông tại S và nằm trong mặt phẳng vuông góc với đáy , hình chiếu vuông góc của S trên đường thẳng AB là điểm H thuộc đoạn AB sao cho BH =2AH .Tính thể tích của khối chóp S.ABCD ?
Cho f'(x)=x2(x+1)(x2+2mx+5). có bao nhiêu giá trị m nguyên, m>-10 để hàm số g(x)=f(\(\left|x\right|\)) có 5 cực trị.
mọi người giúp e câu này vs ạ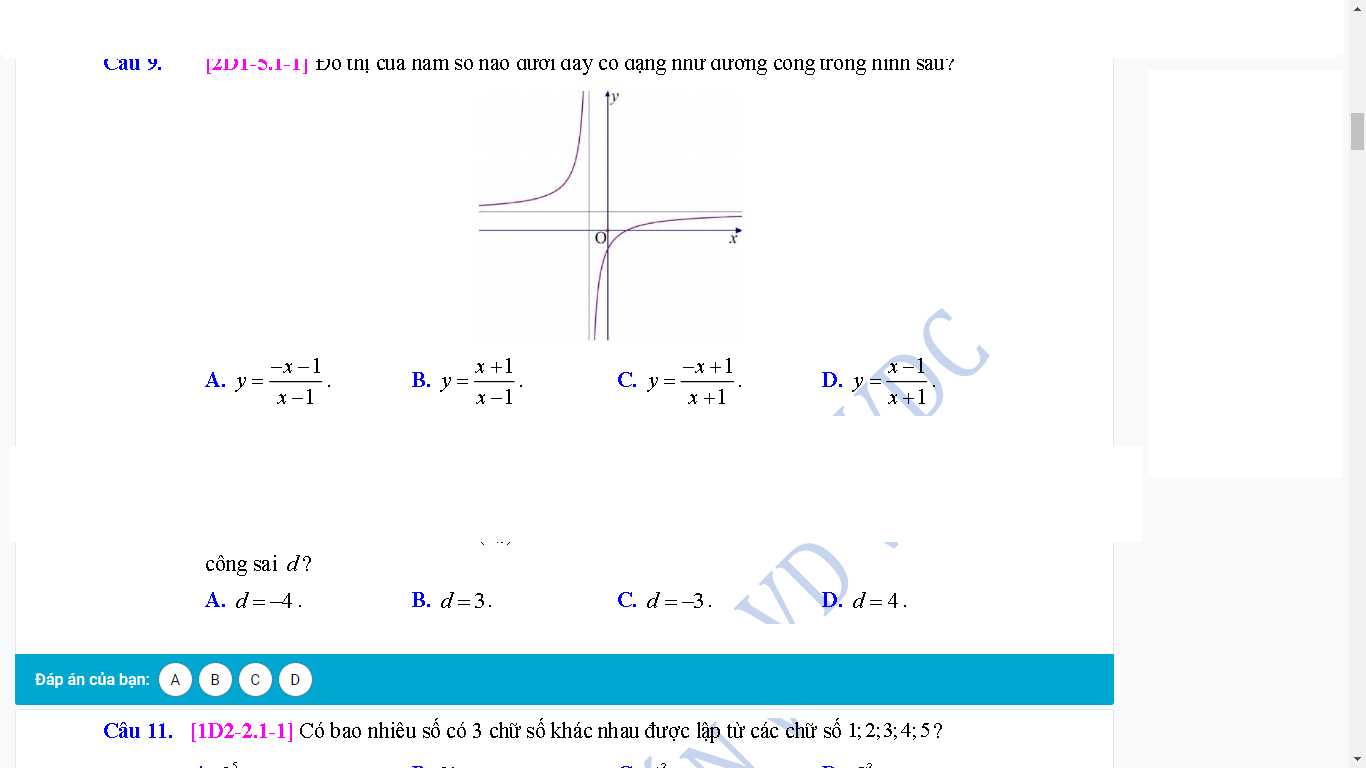
cho x1, x2,...,x5 và \(\sum\limits^5_{i=1}\dfrac{1}{1+x_i}=1.\)Chứng minh rằng \(\sum\limits^5_{i=1}\dfrac{x_i}{a+x_i^2}\le1\)
tìm m để hàm số \(y=x^3+3x^2+\left(m+1\right)x+4m\) nghịch biến trên (-1;1)
tìm m để hàm số \(y=\dfrac{-x^3}{3}+\left(m-2\right)x^2-m\left(m-3\right)x-\dfrac{1}{3}\) nghịch biến trên \(\left(1;+\infty\right)\)
tìm m để hàm số \(y=x^3-\left(m+1\right)x^2-\left(2m^2-3m+2\right)x+2m^2-m\) đồng biến trên \(\left(2;+\infty\right)\)