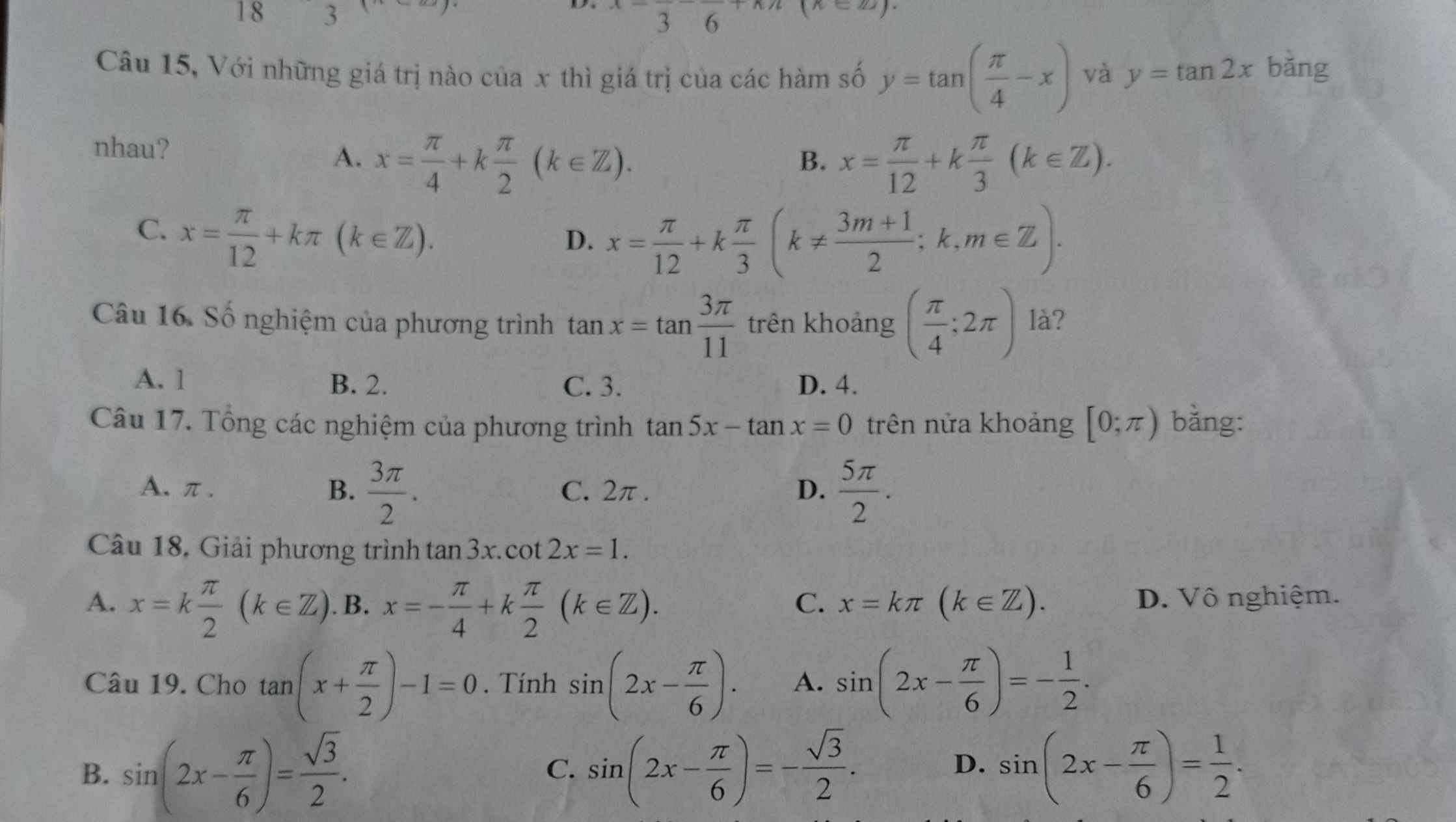Question

15,16,18???

Answer 1

16. ĐKXĐ: $x\neq \frac{\pi}{2}+n\pi$ với $n$ nguyên.

$\tan x=\tan \frac{3\pi}{11}$

$x=\frac{3\pi}{11}+k\pi$ với $k$ nguyên

Vì $\frac{\pi}{4}< \frac{3\pi}{11}+k\pi< 2\pi$

$\Rightarrow -\frac{1}{44}< k< \frac{19}{11}$

Vì $k$ nguyên nên $k=0;1$. Kết hợp ĐKXĐ ta thấy $k=0, 1$ đều thỏa mãn

Tức là số nghiệm của pt là $2$

 

 

Answer 2

15.

ĐKXĐ: $x\neq \frac{3}{4}\pi +n\pi; x\neq \frac{n\pi}{2}-\frac{\pi}{4}$ với $n$ nguyên

\(\tan (\frac{\pi}{4}-x)=\tan 2x\)

\(\Leftrightarrow \frac{\pi}{4}-x=2x+k\pi \) (với $k$ nguyên)

\(\Leftrightarrow x=\frac{\pi}{12}+\frac{k}{3}\pi\) với $k$ nguyên.

Kết hợp với đkxđ suy ra đáp án D. 

Answer 3

17.

ĐKXĐ: $x\neq n\pi +\frac{\pi}{2}; x\neq \frac{n\pi}{5}+\frac{1}{10}\pi$ với $n$ nguyên

$\tan 5x-\tan x=0$
$\Leftrightarrow \tan x=\tan 5x$

$\Leftrightarrow 5x=x+k\pi$ với $k$ nguyên$

$\Leftrightarrow x=\frac{k}{4}\pi$ với $k$ nguyên. 

Vì 0\leq \frac{k\pi}{4}< \pi$

$\Leftrightarrow 0\leq k< 4$

Vì $k$ nguyên nên $k\in \left\{0;1;2;3\right\}$. Kết hợp cùng đkxđ suy ra $k\in\left\{0;1;2;3\right\}$

Tổng các nghiệm của pt:

$\frac{1}{4}\pi (0+1+2+3)=\frac{3}{2}\pi$

Đáp án B.

Answer 4

18.

ĐKXĐ: $x\neq \frac{n\pi}{2}; x\neq \frac{n\pi}{3}-\frac{\pi}{6}$ với $n$ nguyên

\(\tan 3x.\cot 2x=1\Leftrightarrow \tan 3x=\frac{1}{\cot 2x}=\tan 2x\)

\(\Leftrightarrow 3x=2x+k\pi\) với $k$ nguyên

$\Leftrightarrow x=k\pi$ với $k$ nguyên.

Kết hợp với ĐKXĐ suy ra pt vô nghiệm.