a. Ta có
b. Có là hình bình hành ( dấu hiệu nhận biết )
Mặt khác là hình chữ nhật

a. Ta có
b. Có là hình bình hành ( dấu hiệu nhận biết )
Mặt khác là hình chữ nhật
Cho tứ giác ABCD có .Gọi E,F,G,H luần lượt là trung điểm của các cạnh AB,BC,CD,DA
CHứng mỉnh rằng a,OE+OF +OG+OH bằng nữa chu vi tứ giác ABCD,'
b,Tứ giác EFGH là hình chữ nhật
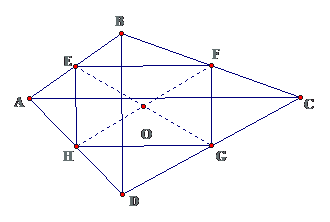
Cho tứ giác ABCD .Gọi EFGH lần lượt là trung điểm của các cạnh AB ,BC,CD,DA.O là giao của 2 đường chéo ,AC vuông goác với BD
Chứng minh rằng :a,OE+OF+OG+OH bằng nửa chu vi tứ giác ABCD
b,Tứ giác AFGH là hình chữ nhật
Cho tứ giác ABCD có .Gọi E,F,G,H luần lượt là trung điểm của các cạnh AB,BC,CD,DA.O là 2 đường chéo
CHứng mỉnh rằng
a,OE+OF +OG+OH bằng nữa chu vi tứ giác ABCD,'
b,Tứ giác EFGH là hình chữ nhật
Cho tứ giác ABCD có AD=BC và AB<CD. Trung điểm của cạnh AB và CD lần lượt là
M và N. Trung điểm của các đường chéo BD và AC lần lượt là P và Q.
a) Chứng minh tứ giác MPNQ là hình thoi
b) Kéo dài hai cạnh DA và CB cắt nhau tại G, kẻ tia phân giác Gx của góc AGB. Chứng
minh Gx//MN.
Cho hình chữ nhật ABCD. Vẽ BH ⊥ AC tại H. Gọi M, O, K lần lượt là trung điểm của AH, BH và CD. Tia CO cắt MB tại E. Tia MO cắt EH và BC lần lượt tại F và N
a, Tứ giác MOCK là hình gì
b, Chứng minh MK ⊥ MB
c, Chứng minh NE . FH = FE . NH
p/s: help em câu c với ạ
Cho hình bình hành ABCD có E, F lần lượt là trung điểm của AB và CD. Gọi giao điểm của AC với DE và BF theo thứ tự là M và N
a) CM: các tứ giác DEBF, EMFN là hình bình hành
b) Hình bình hành ABCD cần thêm điều kiện gì để tứ giác MENF là hình thoi
cho tứ giác ABCD có AC = BD . gọi E, F, G, H lần lượt là trung điểm của BC, AC, AD, DA
C/m tứ giác EFGH là hình thoi