Violympic toán 9
Các câu hỏi tương tự
Cho tam giác ABC nhọn. Hai đường cao BD, CE cắt nhau tại H. Trên HB,HC lần lượt lấy các điểm M và N sao cho \(\widehat{AMC}\) = \(\widehat{ANB}\) = 90°. Chứng minh AM = AN.
B1. Cho tam giác ABC , góc A =90 độ ,AH vuông góc BC
Biết Hb=1,AC=√20.tính Hc
B2. Cho tam giác AbC , góc A 90 độ AH vuông bc , He vuông AB, HF vuông Ac.
C/m: BE.CF.AB.AC=AH^4
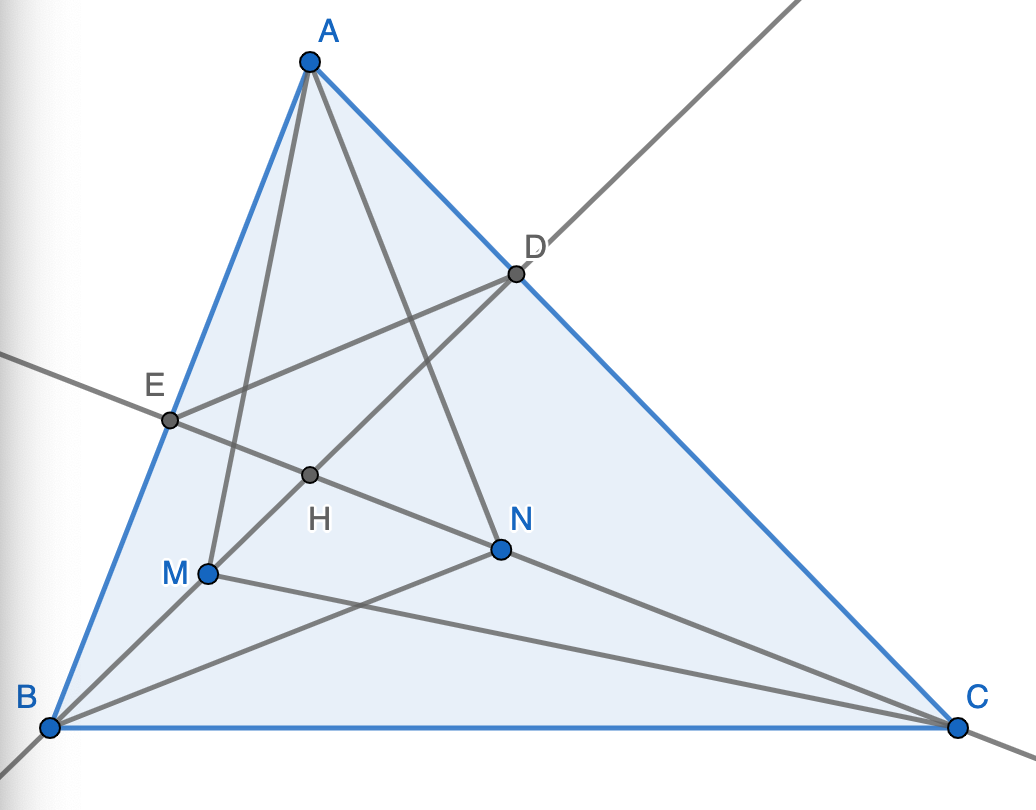
B3. Tam giác AbC nhọn các đường cao BE,Cf cắt tại H. M thuộc Hb ,N thuộc HC sao cho góc Amc=Anb=90 độ
a,cm: AE.Ac=Af.Ab ( đã làm)
b, cm : Am=An
Mk cần gấp ạ :(
Cho tam giác ABC nhọn, ba đường cao AA, BB, CC.
a) CM bigtriangleupACC~bigtriangleupABB (phần này mk lm đc rồi còn các phần còn lại thui giúp vs)
b)Trên BB lấy M, trên CC lấy N sao cho widehat{AMC}widehat{ANB}90^o
CMR: AMAN
c) Gọi S, S lần lượt là diện tích của bigtriangleupABC vàbigtriangleupABC. CMR cos2A+cos2B+cos2C1-dfrac{S}{S}
Đọc tiếp
Cho tam giác ABC nhọn, ba đường cao AA', BB', CC'.
a) CM \(\bigtriangleup\)AC'C~\(\bigtriangleup\)AB'B (phần này mk lm đc rồi còn các phần còn lại thui giúp vs)
b)Trên BB' lấy M, trên CC' lấy N sao cho \(\widehat{AMC}=\widehat{ANB}=90^o\)
CMR: AM=AN
c) Gọi S, S' lần lượt là diện tích của \(\bigtriangleup\)ABC và\(\bigtriangleup\)A'B'C'. CMR cos2A+cos2B+cos2C=1-\(\dfrac{S'}{S}\)
cho tam giác ABC nhọn hai đường cao BD va CE cắt nhau tại H.Vẽ đường tròn tâm O đường kính CH cắt BC tại F
a)
Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn tâm O.Các đường cao BD,CE của tam giác ABC cắt nhau tại H. Đường tròn (I ) ngoại tiếp tam giác BDH cắt đường tròn (O) ở M (M khác B). Vẽ đường kính BF của (O). CMR 3 điểm M, H , F thẳng hàng
Cho hình thang ABCD có \(\widehat{B}=\widehat{C}=90^O\). Hai đường chéo vuông góc với nhau tại H. Biết AB = \(3\sqrt{5}\) cm, HA = 3cm. Chứng minh:
a) HA:HB:HC:HD = 1:2:4:8
b) \(\dfrac{1}{AB^2}-\dfrac{1}{CD^2}=\dfrac{1}{HB^2}-\dfrac{1}{HC^2}\)
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O bán kính R đường cao BD, CE cắt nhau tại H đường thẳng DE cắt đường tròn tâm O tại M và N cắt BC tại K a)chung minh góc AED = góc ACB b) AM = AN c) KE.KD= KB . KC d ) góc BAC = 60° tính diện tích ADOE bằng theo R
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O;R). Hai đường cao BD, CE cắt nhau tại H.
1. Vẽ phân giác của góc BAC cắt BC tại F, cắt (O;R) tại M. CM: AH//OM
2. Tiếp tuyến tại A của đường tròn (O;R) cắt BC tại K, đường thẳng DE cắt KC tại N. CMR: CN.AK = CK. ND
3. Cho góc BAC = 60o vả góc ACB = 45o. Tính AD, AC theo R.
Cho đường tròn tâm O và dây cung BC. Điểm A di chuyển trên cung lớn BC sao cho tam giác ABC có 3 góc nhọn. Đường cao BE, CF của tam giác ABC cắt nhau tại H và cắt đường tròn theo thứ tự tại M và N. Cho cung BC nhỏ có số đo bằng 120 độ. Tính tỉ số diện tích của tam giác AEF và tứ giác BCEF