bài 1 : AC \(=\) gì đấy
\(AC=\frac{1}{2}BC\) nhé.
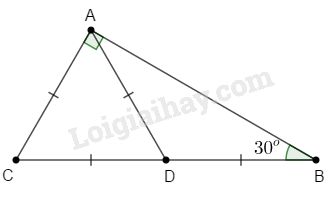
Trên cạnh \(BC\) lấy điểm D sao cho \(CA=CD.\)
+ Vì \(\Delta ABC\) vuông tại \(A\left(gt\right)\)
=> \(\widehat{B}+\widehat{C}=90^0\) (tính chất tam giác vuông).
=> \(30^0+\widehat{C}=90^0\)
=> \(\widehat{C}=90^0-30^0\)
=> \(\widehat{C}=60^0.\)
+ Xét \(\Delta ACD\) có:
\(CA=CD\) (do cách vẽ).
=> \(\Delta ACD\) cân tại C.
Mà \(\widehat{C}=60^0\left(cmt\right)\)
=> \(\Delta ACD\) là tam giác đều.
=> \(\left\{{}\begin{matrix}AC=AD=CD\left(1\right)\\\widehat{CAD}=\widehat{C}=\widehat{ADC}=60^0\end{matrix}\right.\) (tính chất tam giác đều).
Ta có: \(\widehat{CAD}+\widehat{BAD}=\widehat{BAC}\)
=> \(60^0+\widehat{BAD}=90^0\)
=> \(\widehat{BAD}=90^0-60^0\)
=> \(\widehat{BAD}=30^0.\)
Mà \(\widehat{ABD}=30^0\left(gt\right)\)
=> \(\widehat{BAD}=\widehat{ABD}=30^0.\)
=> \(\Delta ABD\) cân tại \(D.\)
=> \(AD=BD\) (tính chất tam giác cân) (2).
Từ (1) và (2) => \(AC=CD=BD.\)
\(CD=BD\)
=> D là trung điểm của \(BC.\)
=> \(CD=BD=\frac{1}{2}BC\) (tính chất trung điểm).
Mà \(AC=CD=BD\left(cmt\right).\)
=> \(AC=\frac{1}{2}BC\left(đpcm\right).\)
Chúc bạn học tốt!













