1/ Cho \(\left|\overrightarrow{u}\right|=\sqrt{2}\) , \(\left|\overrightarrow{v}\right|=10\) , \(\overrightarrow{u}.\overrightarrow{v}=10\). Tính số đó góc hợp giữa \(\overrightarrow{u}và\overrightarrow{v}\) .
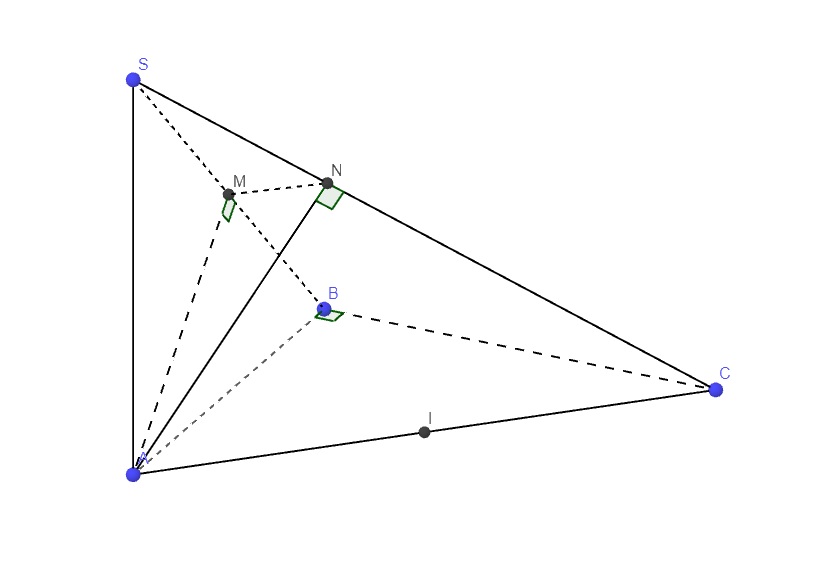
2/ Cho hình chóp S.ABC, đáy là tâm giác vuông cân tại B, SA vuông góc với mặt đáy, AB = SA = a
a. Tính góc 2mp ((SBC),(ABC))
b. Gọi M,N lần lượt là hình chiếu của A lên SB, SC. Tam giác AMN là tam giác gì? tính góc giữa 2mp ((AMN),(ABC)), góc giữa (AC;(AMN)).
c. Tính khoảng cách từ trung điểm I của đoạn thẳng AC đến mp (SBC)
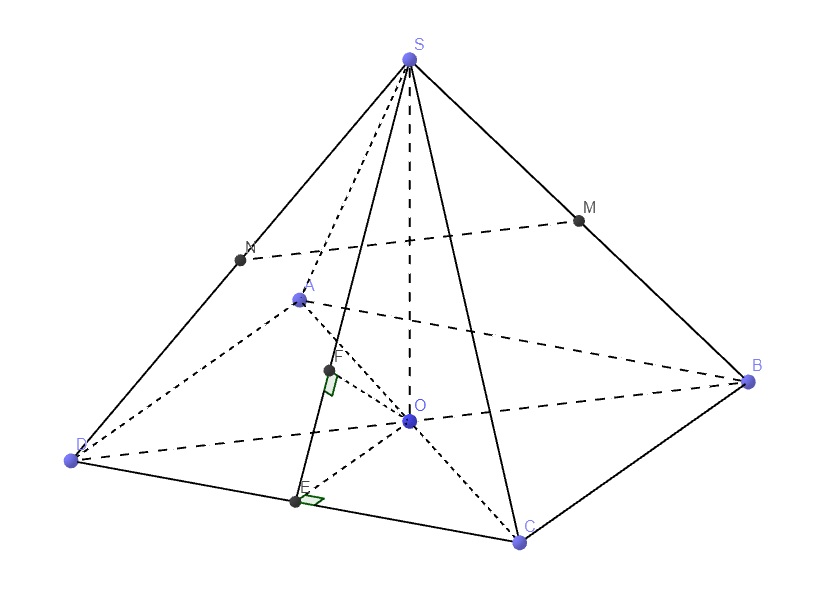
3/ Cho hình chóp S.ABCD, đáy là hình vuống tâm O, SA = SB = SC = SD = AB = 2a. M,N lần lượt là trung điểm SB, SD.
a. Tính số đo của góc giữa (MN;SC)
b. SA vuống góc với đường thẳng nào?
c. Tính a khoảng cách giữa d(AB;(SCD)).
CỨU MK VS, MAI MK KT 15' mà mk lại ko lm đc, ko bt lm lun, giúp mk vs, cảm ơn nhiều.
1.
\(cos\left(\widehat{\overrightarrow{u};\overrightarrow{v}}\right)=\dfrac{\overrightarrow{u}.\overrightarrow{v}}{\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|}=\dfrac{10}{10.\sqrt{2}}=\dfrac{1}{\sqrt{2}}\)
\(\Rightarrow\left(\widehat{\overrightarrow{u};\overrightarrow{v}}\right)=45^0\)
2.
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\) (1)
Mà \(BC=\left(SBC\right)\cap\left(ABC\right)\Rightarrow\widehat{SBA}\) là góc giữa (SBC) và (ABC)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=1\Rightarrow\widehat{SBA}=45^0\)
b.
Từ (1) \(\Rightarrow BC\perp AM\)
Mà \(AM\perp SB\left(gt\right)\) \(\Rightarrow AM\perp\left(SBC\right)\) (2)
\(\Rightarrow AM\perp MN\Rightarrow\Delta AMN\) vuông tại M
Từ (2) \(\Rightarrow AM\perp SC\), mà \(SC\perp AN\left(gt\right)\)
\(\Rightarrow SC\perp\left(AMN\right)\) (3)
Lại có \(SA\perp\left(ABC\right)\) theo giả thiết
\(\Rightarrow\) Góc giữa (AMN) và (ABC) bằng góc giữa SA và SC hay là góc \(\widehat{ASC}\)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{ASC}=\dfrac{AC}{SA}=\sqrt{2}\Rightarrow\widehat{ASC}\approx54^044'\)
Từ (3) \(\Rightarrow AN\) là hình chiếu vuông góc của AC lên (AMN)
\(\Rightarrow\widehat{CAN}\) là góc giữa AC và (AMN)
Mà \(\widehat{CAN}=\widehat{ASC}\) (cùng phụ \(\widehat{ACS}\)) \(\Rightarrow\widehat{CAN}=...\)
c.
\(\left\{{}\begin{matrix}IC=\dfrac{1}{2}AC\left(gt\right)\\AI\cap\left(SBC\right)=C\end{matrix}\right.\) \(\Rightarrow d\left(I;\left(SBC\right)\right)=\dfrac{1}{2}d\left(A;\left(SBC\right)\right)\)
Mà từ (2) ta có \(AM\perp\left(SBC\right)\Rightarrow AM=d\left(A;\left(SBC\right)\right)\)
\(SA=AB\left(gt\right)\Rightarrow\Delta SAB\) vuông cân tại A
\(\Rightarrow AM=\dfrac{1}{2}SB=\dfrac{a\sqrt{2}}{2}\Rightarrow d\left(I;\left(SBC\right)\right)=\dfrac{1}{2}AM=\dfrac{a\sqrt{2}}{4}\)
3.
a.
Do \(SA=SB=SC=SD\Rightarrow\) hình chiếu vuông góc của S lên (ABCD) trùng tâm O của hình vuông
Hay \(SO\perp\left(ABCD\right)\)
\(\Rightarrow SO\perp BD\)
Lại có \(AC\perp BD\) (hai đường chéo hình vuông)
\(\Rightarrow BD\perp\left(SAC\right)\Rightarrow BD\perp SC\)
Mà MN là đường trung bình tam giác SBD \(\Rightarrow MN||BD\)
\(\Rightarrow MN\perp SC\Rightarrow\left(\widehat{MN;SC}\right)=90^0\)
b.
\(AC=\sqrt{AB^2+BC^2}=2a\sqrt{2}\)
\(SA=SC=2a\Rightarrow SA^2+SC^2=8a^2=AC^2\)
\(\Rightarrow\Delta SAC\) vuông tại S (pitago đảo)
\(\Rightarrow SA\perp SC\)
c.
\(AB||CD\Rightarrow AB||\left(SCD\right)\Rightarrow d\left(AB;\left(SCD\right)\right)=d\left(A;\left(SCD\right)\right)\)
Lại có \(\left\{{}\begin{matrix}AC=2OC\\AO\cap\left(SCD\right)=C\end{matrix}\right.\) \(\Rightarrow d\left(A;\left(SCD\right)\right)=2d\left(O;\left(SCD\right)\right)\)
Từ O kẻ \(OE\perp CD\), từ \(O\) kẻ \(OF\perp SE\)
\(\Rightarrow OF\perp\left(SCD\right)\Rightarrow OF=d\left(O;\left(SCD\right)\right)\)
\(OE=\dfrac{1}{2}BC=a\) (đường trung bình)
\(\Delta SAC\) vuông tại S (theo cm câu b) \(\Rightarrow SO=\dfrac{1}{2}AC=a\sqrt{2}\) (trung tuyến ứng với cạnh huyền)
Hệ thức lượng:
\(OF=\dfrac{SO.OE}{\sqrt{SO^2+OE^2}}=\dfrac{a\sqrt{6}}{3}\)
\(\Rightarrow d\left(A;\left(SCD\right)\right)=2OF=\dfrac{2a\sqrt{6}}{3}\)