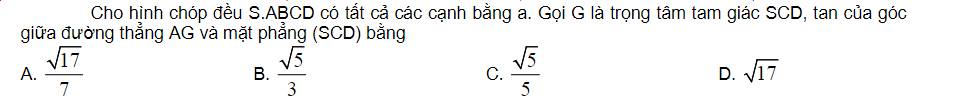Ta có (AG;(SCD) = ^AGD
Cho I là trung điểm CD
Xét tam giác ADI vuông tại D ta có
\(AI=\sqrt{AD^2+DI^2}=\sqrt{a^2+\dfrac{a^2}{4}}=\sqrt{\dfrac{5a^2}{4}}=\dfrac{\sqrt{5}a}{2}\)
Xét tam giác SCD có SI là đường trung tuyến vừa là đường cao
\(SI=\dfrac{a\sqrt{3}}{2}\)( do SI là đường cao trong tam giác đều )
Xét tam giác SAI ta có
cos^SIA = \(\dfrac{SI^2+AI^2-SA^2}{2.SI.AI}=\dfrac{\dfrac{a^2.3}{4}+\dfrac{5a^2}{4}-a^2}{\dfrac{2.\sqrt{15}a^2}{4}}=\dfrac{2\sqrt{15}}{15}\)
Xét tam giác AGI có
\(\dfrac{2\sqrt{15}}{15}=\dfrac{AI^2+GI^2-AG^2}{2.AI.GI}\Leftrightarrow AG^2=a^2\)
Xét tam giác AGD có
cos^AGD = \(\dfrac{AG^2+GD^2-AD^2}{2.AG.GD}=\dfrac{\sqrt{3}}{6}\)
=> tan ^AGD = \(\sqrt{11}\)