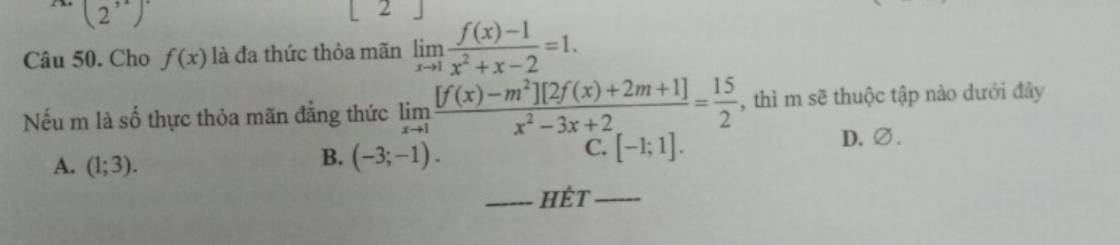Giả thiết suy ra \(f\left(1\right)=1\)
Giới hạn \(\dfrac{\left[f\left(x\right)-m^2\right].\left[2f\left(x\right)+2m+1\right]}{x^2-3x+2}\) hữu hạn nên \(\left[f\left(x\right)-m^2\right]\left[2f\left(x\right)+2m+1\right]=0\) có nghiệm \(x=1\)
\(\Rightarrow\left[f\left(1\right)-m^2\right].\left[2f\left(1\right)+2m+1\right]=0\)
\(\Rightarrow\left(1-m^2\right)\left(2m+3\right)=0\)
\(\Rightarrow m=\left\{-\dfrac{3}{2};-1;1\right\}\)
Lần lượt thay 3 giá trị ta được \(m=-\dfrac{3}{2}\) thỏa mãn (đến đoạn này biện pháp tốt nhất là chọn hàm \(f\left(x\right)=x^2+x-1\) rồi CALC là 3s xong kết quả chứ tính tay 3 con giới hạn chắc hết ngày)