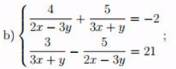b: \(\left\{{}\begin{matrix}\dfrac{4}{2x-3y}+\dfrac{5}{3x+y}=-2\\\dfrac{3}{3x+y}-\dfrac{5}{2x-3y}=21\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{4}{2x-3y}+\dfrac{5}{3x+y}=-2\\\dfrac{5}{2x-3y}-\dfrac{3}{3x+y}=-21\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{12}{2x-3y}+\dfrac{15}{3x+y}=-6\\\dfrac{25}{2x-3y}-\dfrac{15}{3x+y}=-105\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{37}{2x-3y}=-111\\\dfrac{12}{2x-3y}+\dfrac{15}{3x+y}=-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-3y=-\dfrac{1}{3}\\\dfrac{15}{3x+y}=-6-\dfrac{12}{2x-3y}=-6-12:\dfrac{-1}{3}=-6+36=30\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-3y=-\dfrac{1}{3}\\3x+y=\dfrac{1}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-3y=-\dfrac{1}{3}\\9x+3y=\dfrac{3}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}11x=-\dfrac{1}{3}+\dfrac{3}{2}=\dfrac{-2+9}{6}=\dfrac{7}{6}\\2x-3y=-\dfrac{1}{3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{7}{66}\\3y=2x+\dfrac{1}{3}=\dfrac{7}{33}+\dfrac{1}{3}=\dfrac{7+11}{33}=\dfrac{18}{33}=\dfrac{6}{11}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{7}{66}\\y=\dfrac{2}{11}\end{matrix}\right.\)
Gọi \(\left\{{}\begin{matrix}\dfrac{1}{2x-3y}=A\\\dfrac{1}{3x+y}=B\end{matrix}\right.\)
Hệ đây nha
\(\left\{{}\begin{matrix}4A+5B=2\\3B-5A=21\end{matrix}\right.\)
xong giải hệ như bình thường
giải A,B xong r thay kết quả
\(\left\{{}\begin{matrix}\dfrac{1}{x}=KếtquảcủaA\\\dfrac{1}{y}=kếtquảcủaB\end{matrix}\right.\)
Nếu tử =1 thì bằng luôn kết quả
Nếu tử \(\ne1\) thì nhân chéo
Sau đó lại giải hệ lần 2 và kế luật