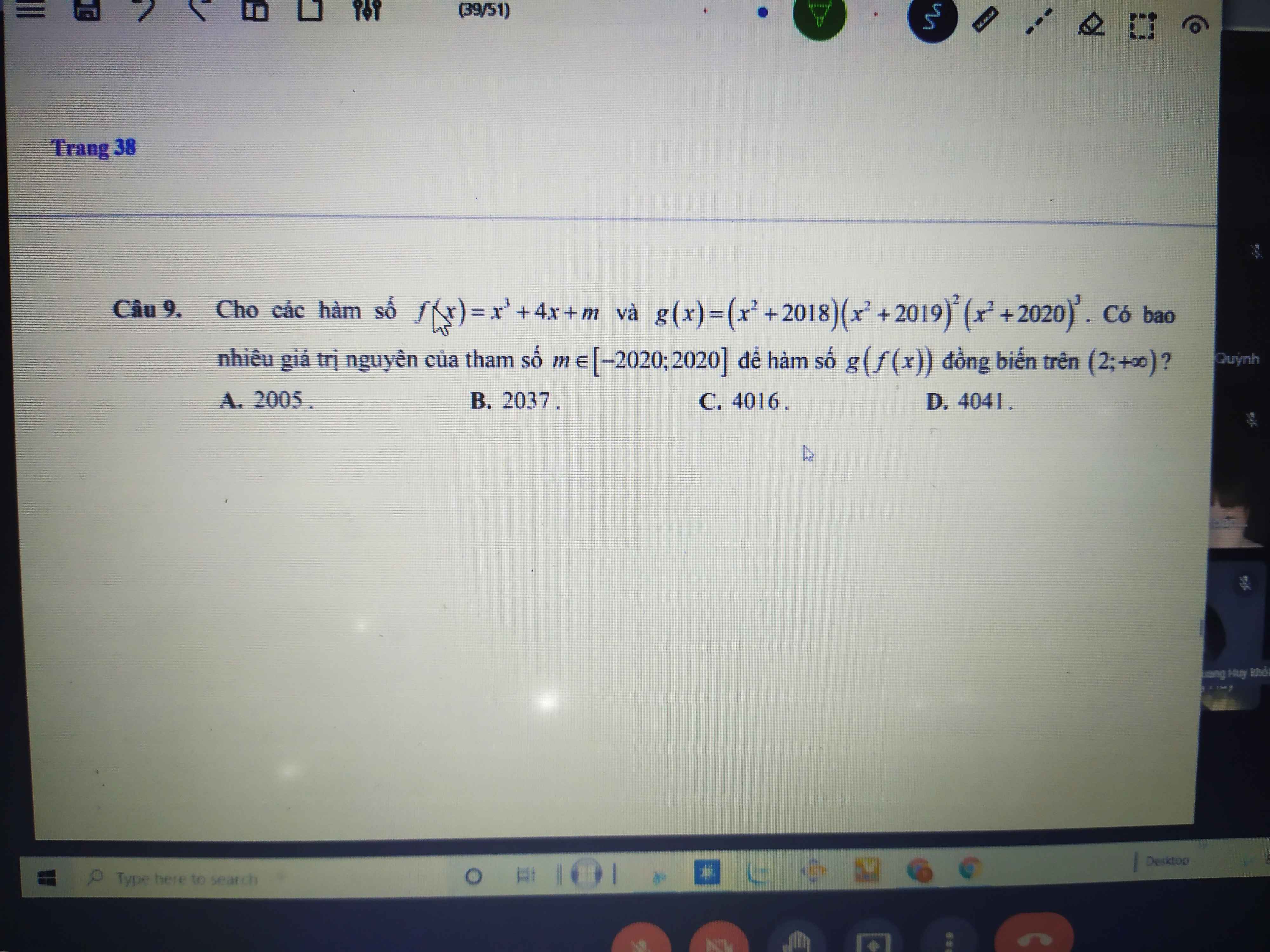
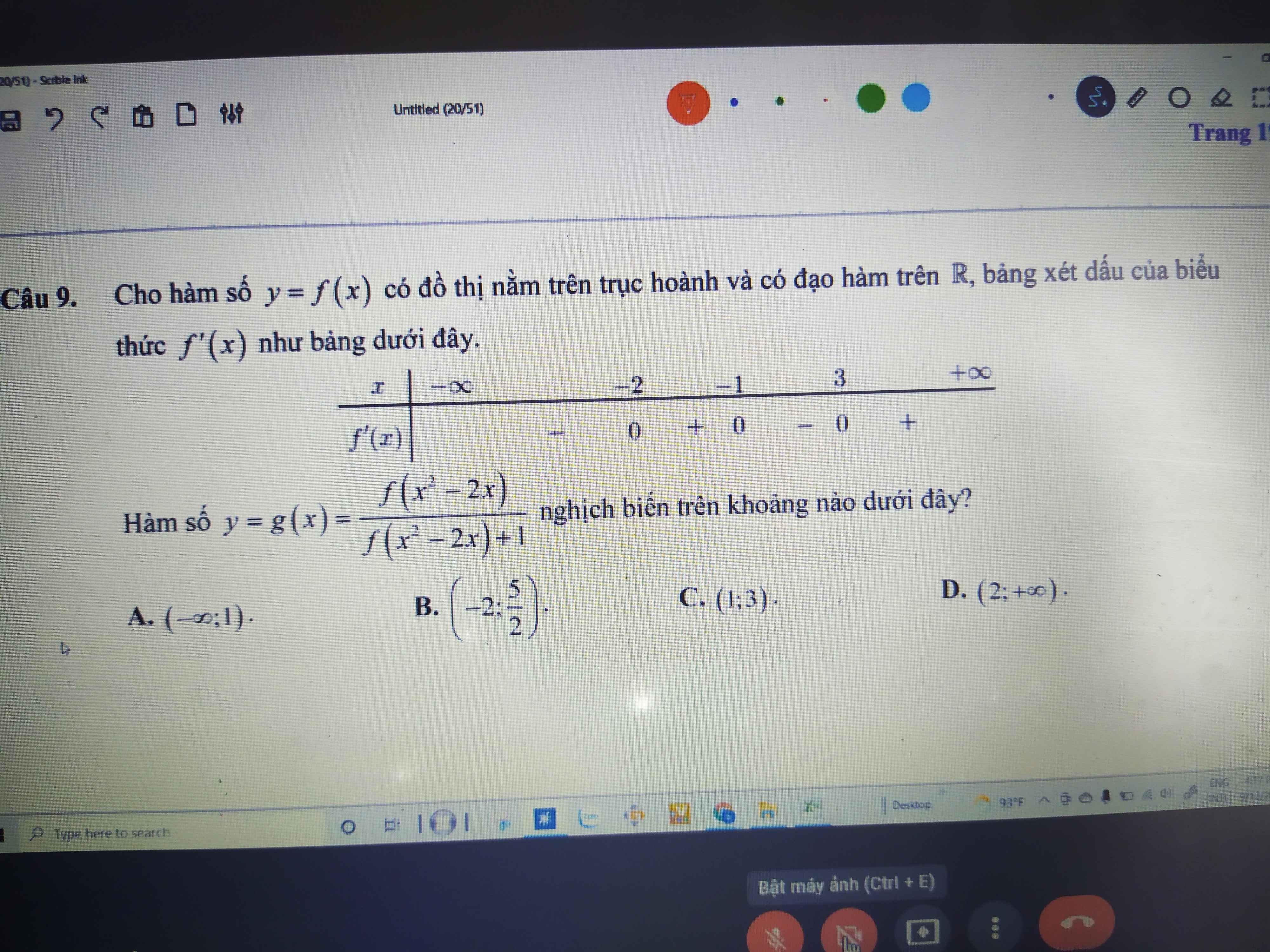
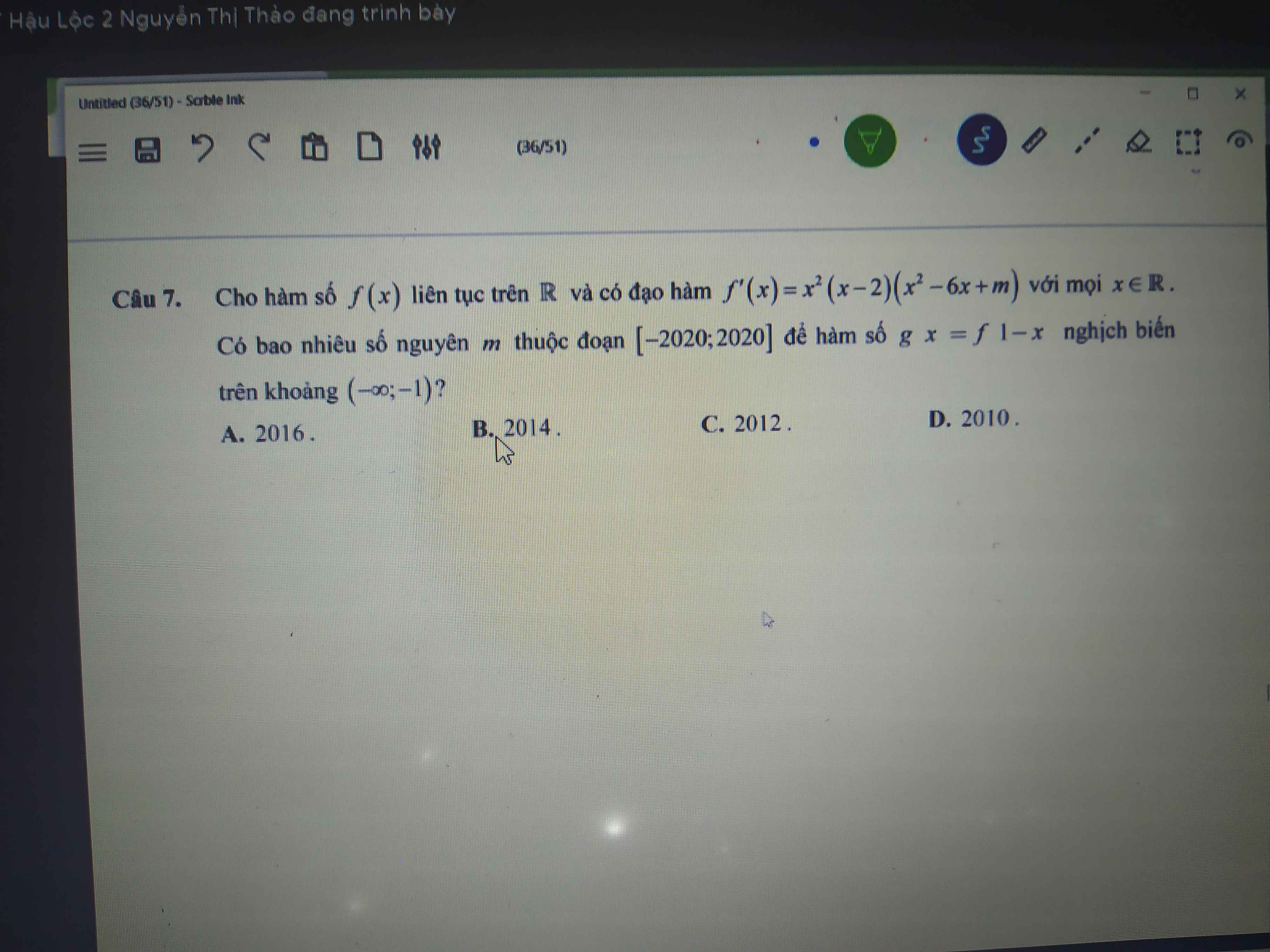
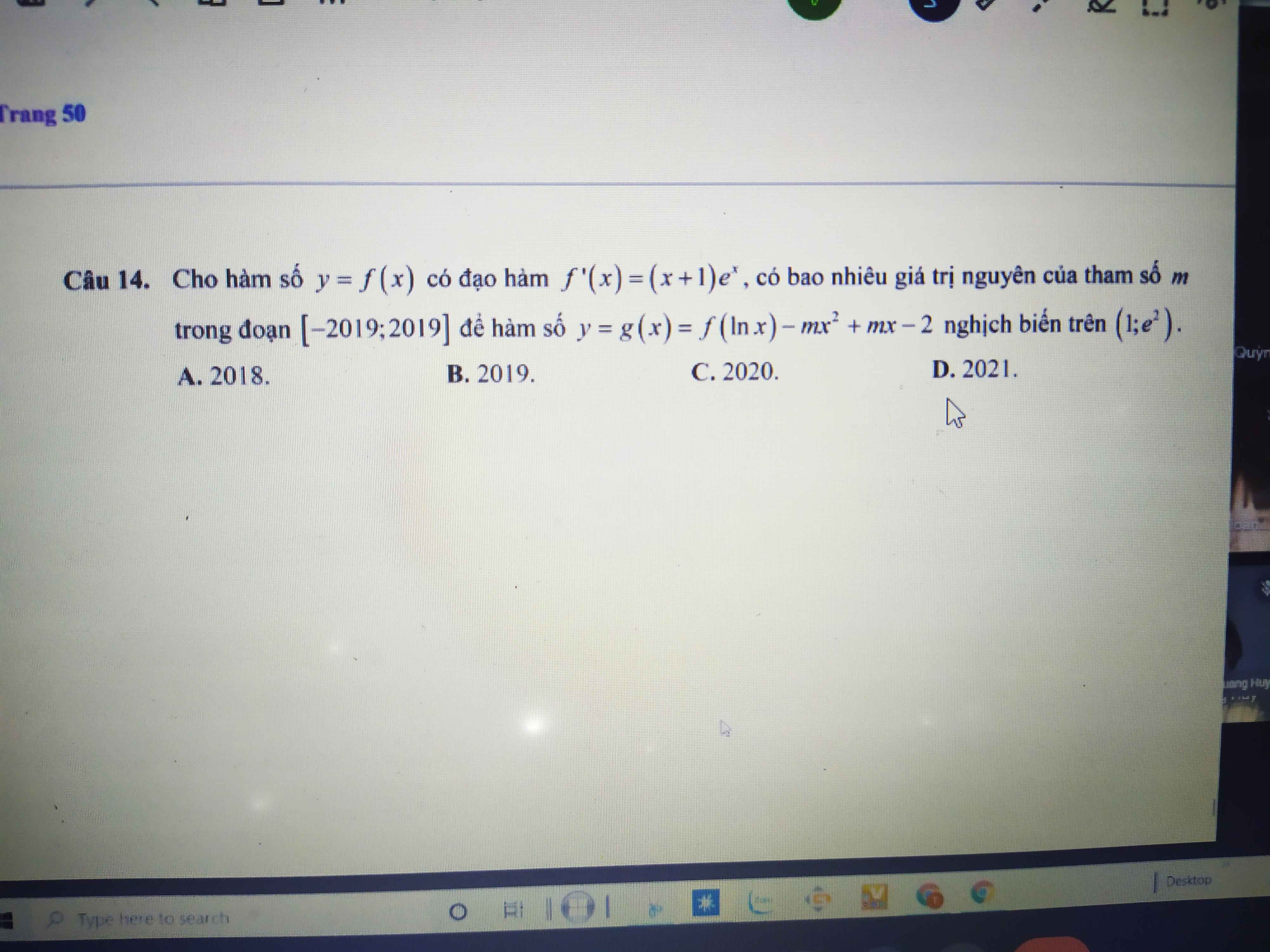
TXĐ: D=R\{m}
\(y=\dfrac{mx-m-6}{x-m}\)
=>\(y'=\dfrac{\left(mx-m-6\right)'\left(x-m\right)-\left(mx-m-6\right)\left(x-m\right)'}{\left(x-m\right)^2}\)
=>\(y'=\dfrac{m\left(x-m\right)-\left(mx-m-6\right)}{\left(x-m\right)^2}\)
=>\(y'=\dfrac{mx-m^2-mx+m+6}{\left(x-m\right)^2}=\dfrac{-m^2+m+6}{\left(x-m\right)^2}\)
Để hàm số đồng biến trên từng tập xác định thì \(y'>0\forall x\)
=>\(-m^2+m+6>0\)
\(\Leftrightarrow m^2-m-6< 0\)
=>(m-3)(m+2)<0
TH1: \(\left\{{}\begin{matrix}m+2>0\\m-3< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>-2\\m< 3\end{matrix}\right.\)
=>-2<m<3
TH2: \(\left\{{}\begin{matrix}m+2< 0\\m-3>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m< -2\\m>3\end{matrix}\right.\)
=>Loại
Vậy: -2<m<3
=>S={-1;0;1;2}
=>Chọn B