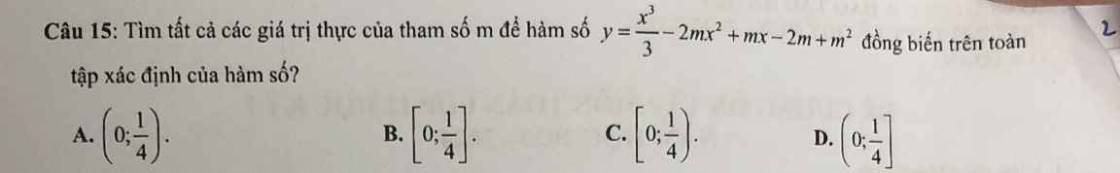TXĐ: D=R
\(y=\dfrac{1}{3}x^3-2mx^2+mx-2m+m^2\)
=>\(y'=\dfrac{1}{3}\cdot3x^2-2m\cdot2x+m=x^2-4mx+m\)
Để hàm số đồng biến trên toàn TXĐ của nó thì \(y'>=0\forall x\)
=>\(\left\{{}\begin{matrix}\text{Δ}< =0\\a>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(4m\right)^2-4m< =0\\1>0\end{matrix}\right.\)
=>\(16m^2-4m< =0\)
=>\(4m^2-m< =0\)
=>m(4m-1)<=0
TH1: \(\left\{{}\begin{matrix}m>=0\\4m-1< =0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>=0\\m< =\dfrac{1}{4}\end{matrix}\right.\)
=>0<=m<=1/4
TH2: \(\left\{{}\begin{matrix}m< =0\\4m-1>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m< =0\\m>=\dfrac{1}{4}\end{matrix}\right.\)
=>Loại
=>Chọn B