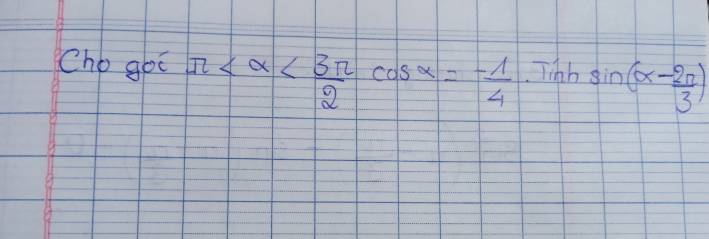\(\pi< \alpha< \dfrac{3\pi}{2}\Rightarrow sin\alpha< 0\)\(\Rightarrow sin\alpha=-\sqrt{1-cos^2\alpha}=\dfrac{-\sqrt{15}}{4}\)
\(sin\left(\alpha-\dfrac{2\pi}{3}\right)=sin\alpha.cos\dfrac{2\pi}{3}-cos\alpha.sin\dfrac{2\pi}{3}\)
\(=\dfrac{-\sqrt{15}}{4}.\dfrac{-1}{2}-\dfrac{-1}{4}.\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{15}+\sqrt{3}}{8}\)
Mọi người ơi câu này phải hạ bậc hay là có thể căn bậc hai \(\sin^22x\) ạ
Giải phương trình:
\(\sin^22x=1\)
Thanks mọi người!
trong mp Oxy cho điểm M(-2;4. ảnh của M qua hai phép liên tiếp V(0;-2) và ĐOy
Với giá trị nào của m thì pt \(cosx\left(2cosx-m\right)+4cosx=2m\) vô nghiệm
Giải giúp mình phương trình này với :
\(2\cos x+\left(\sqrt{3}+4\right)\sin x=2\)
Trong mặt phẳng Oxy cho 2 điểm A(0,1);B(-2,0). Tìm ảnh A' ; B' qua phép quay tâm O góc quay 90
Bài 1: Với giá trị nào của tham số m thì phương trình \(\sqrt{2}sin3x-m+1=0\) vô nghiệm
Bài 2: Phương trình \(ta\left(2x-\frac{\pi}{3}\right)=\sqrt{3}\) có bao nhiêu nghiệm nguyên thuộc khoảng \(\left(0;5\pi\right)\)
Giải chi tiết giúp e vs ạ
