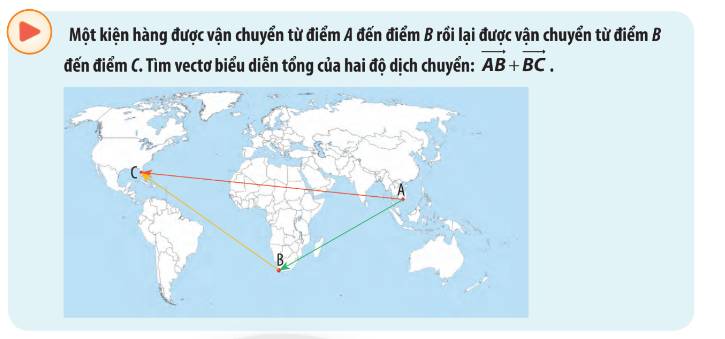
\(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Bài 2: Tổng và hiệu của hai vectơ
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Một robot thực hiện liên tiếp hai chuyển động có độ dịch chuyển lần lượt được biểu diễn bởi 2 vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) (Hình 1). Tìm vectơ biểu diễn sự dịch chuyển của rô bốt sau hai sự dịch chuyển trên.
Cho hình bình hành ABCD (Hình 4). Chứng minh rằng: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)

Hai người cùng kéo một con thuyền với hai lực \(\overrightarrow {{F_1}} = \overrightarrow {OA} ,\overrightarrow {{F_2}} = \overrightarrow {OB} \) có độ lớn lần lượt là 400 N, 600 N (hình 8). Cho biết góc giữa hai vectơ là \({60^\circ }\). Tìm độ lớn của vectơ hợp lực \(\overrightarrow F \) là tổng của hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \)
Cho hình vuông ABCD có cạnh bằng 1 và một điểm O tùy ý. Tính độ dài của các vectơ sau:
a) \(\overrightarrow a = \overrightarrow {OB} - \overrightarrow {OD} ;\)
b) \(\overrightarrow b = \left( {\overrightarrow {OC} - \overrightarrow {OA} } \right) + \left( {\overrightarrow {DB} - \overrightarrow {DC} } \right)\).
Cho 3 vectơ overrightarrow a ,overrightarrow b ,overrightarrow c được biểu diễn như hình 9. Hãy hoàn thành các phép cộng vectơ sau và so sánh kết quả tìm được:a) overrightarrow a + overrightarrow b overrightarrow {AB} + overrightarrow {BC} ?overrightarrow b + overrightarrow a overrightarrow {AE} + overrightarrow {EC} ?b) left( {overrightarrow a + overrightarrow b } right) + overrightarrow c left( {overrightarrow {AB} + overrightarrow {BC} } right) + overrightarrow {CD} overrig...
Đọc tiếp
Cho 3 vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) được biểu diễn như hình 9. Hãy hoàn thành các phép cộng vectơ sau và so sánh kết quả tìm được:
a) \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = ?\)
\(\overrightarrow b + \overrightarrow a = \overrightarrow {AE} + \overrightarrow {EC} = ?\)
b) \(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \overrightarrow {CD} = \overrightarrow {AC} + \overrightarrow {CD} = ?\)
\(\overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right) = \overrightarrow {AB} + \left( {\overrightarrow {BC} + \overrightarrow {CD} } \right) = \overrightarrow {AB} + \overrightarrow {BD} = ?\)

Cho hình vuông ABCD có cạnh bằng 1. Tính độ dài các vectơ sau:
a) \(\overrightarrow a = \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right) + \overrightarrow {CB} ;\)
b) \(\overrightarrow a = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {BC} + \overrightarrow {DA} .\)
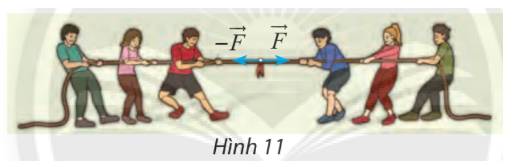
Tìm hợp lực của hai lực đối nhau \(\overrightarrow F \) và \( - \overrightarrow F \) (hình 11)
Cho hình bình hành ABCD có O là giao điểm hai đường chéo và một điểm M tùy ý. Chứng minh rằng:
a) \(\overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow {0;} \)
b) \(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} \)
Cho tam giác đều ABC cạnh bằng a. Tính độ dài các vectơ:
a) \(\overrightarrow {BA} + \overrightarrow {AC} \);
b) \(\overrightarrow {AB} + \overrightarrow {AC} \);
c) \(\overrightarrow {BA} - \overrightarrow {BC} \).
Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Chứng minh rằng:
a) \(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {OD} - \overrightarrow {OC;} \)
b) \(\overrightarrow {OA} - \overrightarrow {OB} + \overrightarrow {DC} = \overrightarrow 0 \)