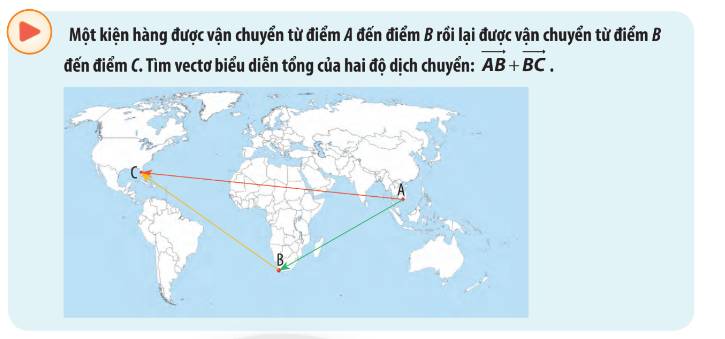
Bài 2: Tổng và hiệu của hai vectơ
Khởi động (SGK Chân trời sáng tạo trang 88-90)
Thảo luận (1)
Khám phá 1 (SGK Chân trời sáng tạo trang 88-90)
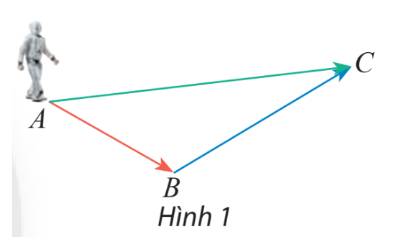
Một robot thực hiện liên tiếp hai chuyển động có độ dịch chuyển lần lượt được biểu diễn bởi 2 vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) (Hình 1). Tìm vectơ biểu diễn sự dịch chuyển của rô bốt sau hai sự dịch chuyển trên.
Thảo luận (1)Hướng dẫn giảiTa thấy rô bốt đi từ A đến B, sau đó đi từ B đến C, vậy cả 2 lần di chuyển thì ta thấy điểm cuất phát là A và điểm kết thúc là C.
Suy ra vectơ biểu diễn sự dịch chuyển của rô bốt sau hai lần dịch chuyển là vectơ \(\overrightarrow {AC} \)
(Trả lời bởi Hà Quang Minh)
Khám phá 2 (SGK Chân trời sáng tạo trang 88-90)
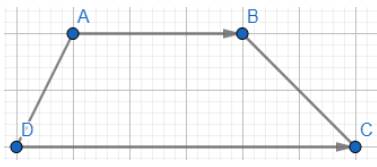
Cho hình bình hành ABCD (Hình 4). Chứng minh rằng: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)

Thảo luận (1)Hướng dẫn giảiVì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (đpcm)
(Trả lời bởi Hà Quang Minh)
Thực hành 1 (SGK Chân trời sáng tạo trang 88-90)
Cho hình thang ABCD có đáy là AB và CD. Cho biết \(\overrightarrow a = \overrightarrow {AC} + \overrightarrow {CB} ;\overrightarrow b = \overrightarrow {DB} + \overrightarrow {BC} \). Chứng minh rằng hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.
Thảo luận (1)Hướng dẫn giải
Áp dụng quy tắc ba điểm ta có:
\(\overrightarrow a = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \); \(\overrightarrow b = \overrightarrow {DB} + \overrightarrow {BC} = \overrightarrow {DC} \)
Mà ABCD là hình thang nên AB//DC. Mặt khác vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \) đều có hướng từ trái sang phải, suy ra vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \)cùng hướng
Vậy hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.
(Trả lời bởi Hà Quang Minh)
Thực hành 2 (SGK Chân trời sáng tạo trang 88-90)
Cho tam giác đều ABC cạnh có độ dài là a. Tính độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC}\)
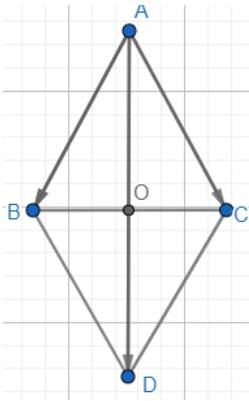
Thảo luận (1)Hướng dẫn giảiDựng hình bình hành ABDC.
Áp dụng quy tắc hình bình hành vào ABDC ta có:
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)
Gọi O là giao điểm của AD và BC, ta có:
\(AO = \sqrt {A{B^2} - B{O^2}} = \sqrt {A{B^2} - {{\left( {\frac{1}{2}BC} \right)}^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
\(AD = 2AO = a\sqrt 3 \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3 \)
Vậy độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \) là \(a\sqrt 3 \)
(Trả lời bởi Hà Quang Minh)
Vận dụng 1 (SGK Chân trời sáng tạo trang 88-90)
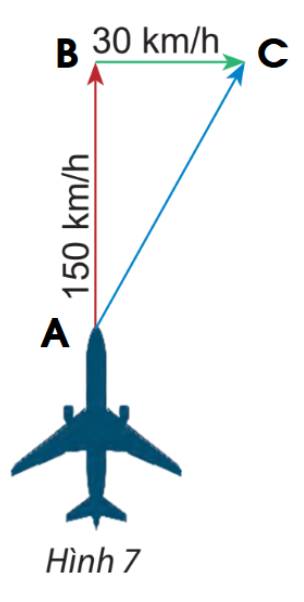
Một máy bay có vận tốc chỉ theo hướng bắc, vận tốc gió là một vectơ theo hướng đông như hình 7. Tính độ dài vectơ tổng của hai vectơ nói trên.

Thảo luận (1)Hướng dẫn giảiGọi vectơ chỉ vận tốc của máy bay là vectơ \(\overrightarrow {AB} \) và vectơ chỉ vận tốc của gió là vectơ \(\overrightarrow {BC} \).
Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Áp dụng định lý Pitago ta có:
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{150}^2} + {{30}^2}} = 30\sqrt {26} \)
Vậy độ dài vectơ tổng của hai vectơ nói trên là \(30\sqrt {26} \) km/h
(Trả lời bởi Hà Quang Minh)
Vận dụng 2 (SGK Chân trời sáng tạo trang 88-90)
Hai người cùng kéo một con thuyền với hai lực \(\overrightarrow {{F_1}} = \overrightarrow {OA} ,\overrightarrow {{F_2}} = \overrightarrow {OB} \) có độ lớn lần lượt là 400 N, 600 N (hình 8). Cho biết góc giữa hai vectơ là \({60^\circ }\). Tìm độ lớn của vectơ hợp lực \(\overrightarrow F \) là tổng của hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \)
Thảo luận (1)Hướng dẫn giải
Áp dụng quy tắc hình bình hành ta có: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} \);
\(AC = OB = 600\); \(\widehat {AOB} = 60^\circ \Rightarrow \widehat {OAC} = 120^\circ \) (hai góc bù nhau trong hình bình hành).
Áp dụng định lý cos ta có:
\(OC = \sqrt {O{A^2} + A{C^2} - 2OA.AC.\cos (120^\circ )} \)
\( = \sqrt {{{400}^2} + {{600}^2} - 2.400.600.\cos (120^\circ )} \simeq 871,78\)N
Vậy độ lớn của vectơ hợp lực \(\overrightarrow F \) gần bằng 871,78 N.
(Trả lời bởi Hà Quang Minh)
Khám phá 2 (SGK Chân trời sáng tạo trang 88-90)
Cho 3 vectơ overrightarrow a ,overrightarrow b ,overrightarrow c được biểu diễn như hình 9. Hãy hoàn thành các phép cộng vectơ sau và so sánh kết quả tìm được:a) overrightarrow a + overrightarrow b overrightarrow {AB} + overrightarrow {BC} ?overrightarrow b + overrightarrow a overrightarrow {AE} + overrightarrow {EC} ?b) left( {overrightarrow a + overrightarrow b } right) + overrightarrow c left( {overrightarrow {AB} + overrightarrow {BC} } right) + overrightarrow {CD} overrig...
Đọc tiếp
Cho 3 vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) được biểu diễn như hình 9. Hãy hoàn thành các phép cộng vectơ sau và so sánh kết quả tìm được:
a) \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = ?\)
\(\overrightarrow b + \overrightarrow a = \overrightarrow {AE} + \overrightarrow {EC} = ?\)
b) \(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \overrightarrow {CD} = \overrightarrow {AC} + \overrightarrow {CD} = ?\)
\(\overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right) = \overrightarrow {AB} + \left( {\overrightarrow {BC} + \overrightarrow {CD} } \right) = \overrightarrow {AB} + \overrightarrow {BD} = ?\)

Thảo luận (1)Hướng dẫn giảia) Áp dụng quy tắc ba điểm ta có:
\(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \);
\(\overrightarrow b + \overrightarrow a = \overrightarrow {AE} + \overrightarrow {EC} = \overrightarrow {AC} \)
\( \Rightarrow \overrightarrow a + \overrightarrow b = \overrightarrow b + \overrightarrow a \)
b) Áp dụng quy tắc ba điểm ta có:
\(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \overrightarrow {CD} = \overrightarrow {AC} + \overrightarrow {CD} = \overrightarrow {AD} \)
\(\overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right) = \overrightarrow {AB} + \left( {\overrightarrow {BC} + \overrightarrow {CD} } \right) = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \)
\( \Rightarrow \left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)\)
(Trả lời bởi Hà Quang Minh)
Thực hành 3 (SGK Chân trời sáng tạo trang 88-90)
Cho hình vuông ABCD có cạnh bằng 1. Tính độ dài các vectơ sau:
a) \(\overrightarrow a = \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right) + \overrightarrow {CB} ;\)
b) \(\overrightarrow a = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {BC} + \overrightarrow {DA} .\)
Thảo luận (1)Hướng dẫn giảia) \(\begin{array}{l}\overrightarrow a = \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right) + \overrightarrow {CB} = \left( {\overrightarrow {AC} + \overrightarrow {CB} } \right) + \overrightarrow {BD} \\ = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD}\\ \Rightarrow |{\overrightarrow a}|= \left| {\overrightarrow {AD} } \right| = AD = 1\end{array}\)
b) \(\begin{array}{l}\overrightarrow a = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {BC} + \overrightarrow {DA} = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \left( {\overrightarrow {AD} + \overrightarrow {DA} } \right)\\ = \overrightarrow {AC} + \overrightarrow {AA} = \overrightarrow {AC} + \overrightarrow 0 = \overrightarrow {AC} \end{array}\)
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{1^2} + {1^2}} = \sqrt 2 \)
\(\Rightarrow |{\overrightarrow a}|= \left| {\overrightarrow {AC} } \right| = \sqrt 2 \)
(Trả lời bởi Hà Quang Minh)
Khám phá 3 (SGK Chân trời sáng tạo trang 91,92)
Tìm hợp lực của hai lực đối nhau \(\overrightarrow F \) và \( - \overrightarrow F \) (hình 11)
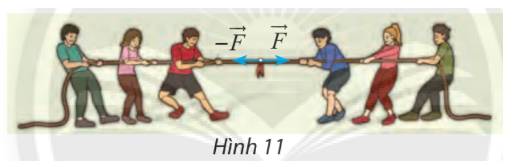
Thảo luận (1)Hướng dẫn giải\( \overrightarrow F + \left( { - \overrightarrow F } \right) =\overrightarrow F - \overrightarrow F = \overrightarrow 0 \)
(Trả lời bởi Hà Quang Minh)