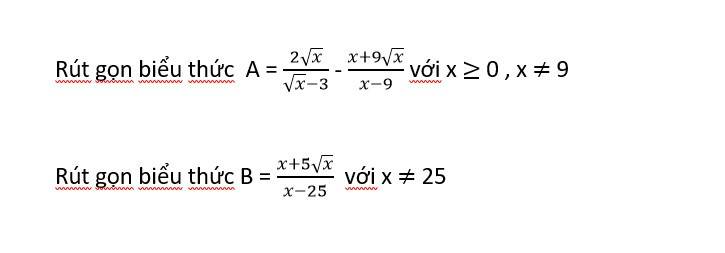\(A=\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{x+9\sqrt{x}}{x-9}\left(dkxd:x\ge0,x\ne9\right)\\ =\dfrac{2\sqrt{x}\left(\sqrt{x}+3\right)-\left(x+9\sqrt{x}\right)}{x-9}\\ =\dfrac{2x+6\sqrt{x}-x-9\sqrt{x}}{x-9}\\ =\dfrac{x-3\sqrt{x}}{x-9}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ =\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
\(B=\dfrac{x+5\sqrt{x}}{x-25}\left(dkxd:x\ne25,x\ge0\right)\\ =\dfrac{\sqrt{x}\left(\sqrt{x}+5\right)}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)} \\ =\dfrac{\sqrt{x}}{\sqrt{x}-5}\)
Đúng 1
Bình luận (0)
