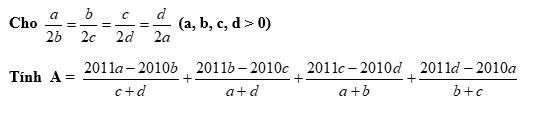Question

Answer 1

\(\dfrac{a}{2b}=\dfrac{b}{2c}=\dfrac{c}{2d}=\dfrac{d}{2a}=\dfrac{a+b+c+d}{2b+2c+2d+2a}=\dfrac{1}{2}\)

\(\Rightarrow\left\{{}\begin{matrix}a=b\\b=c\\c=d\\d=a\end{matrix}\right.\) \(\Rightarrow a=b=c=d\)

\(\Rightarrow A=\dfrac{2011a-2010a}{a+a}+\dfrac{2011a-2010a}{a+a}+\dfrac{2011a-2010a}{a+a}+\dfrac{2011a-2010a}{a+a}=2\)