\(B=\dfrac{x^2-x+5}{x^2-x+1}=1+\dfrac{4}{\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}}\)
\(\left(x-\dfrac{1}{2}\right)^2\ge0\)
\(\Rightarrow\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\Rightarrow\dfrac{1}{\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}}\le\dfrac{4}{3}\)
\(\Rightarrow\dfrac{4}{\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}}\le\dfrac{16}{3}\)
\(\Rightarrow B\le\dfrac{19}{3}\)
Dấu "=" xảy ra khi \(x-\dfrac{1}{2}=0\Leftrightarrow x=\dfrac{1}{2}\)
Vậy giá trị lớn nhất của B là \(\dfrac{19}{3}\) khi \(x=\dfrac{1}{2}\).
















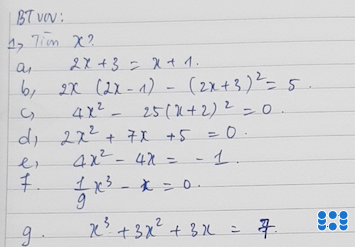

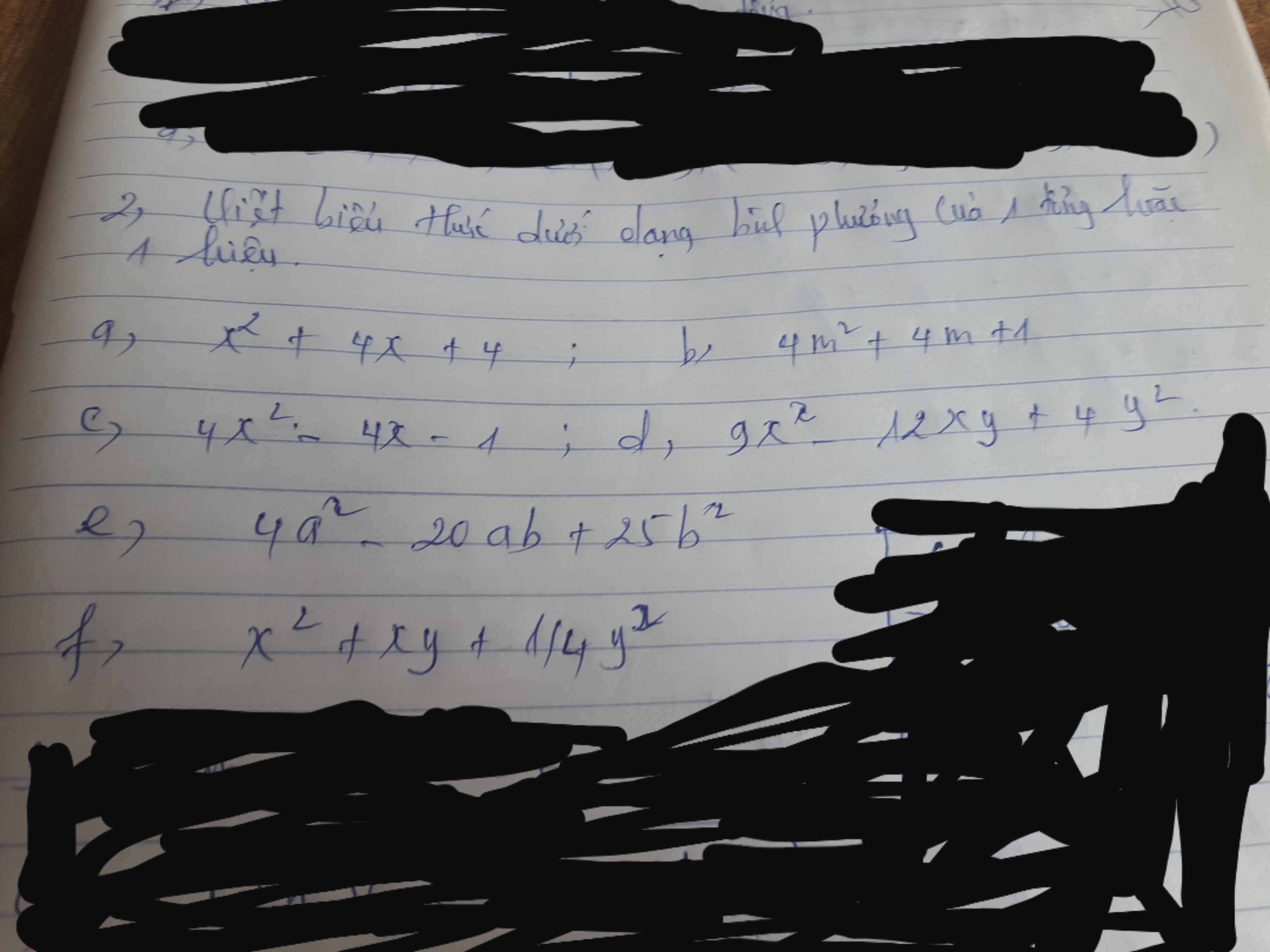



 giải thích giùm mình với
giải thích giùm mình với