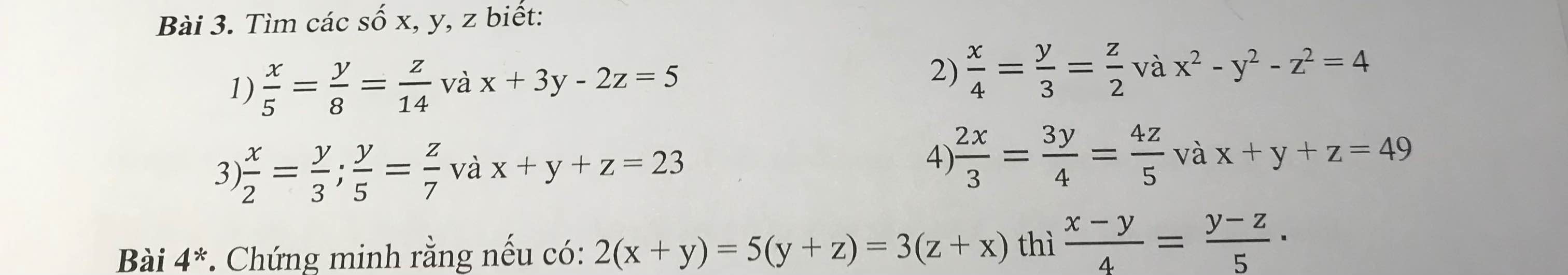1: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{5}=\dfrac{y}{8}=\dfrac{z}{14}=\dfrac{x+3y-2z}{5+3\cdot8-2\cdot14}=\dfrac{5}{1}=5\)
=>x=25; y=40; z=70
2: Đặt x/4=y/3=z/2=k
=>x=4k; y=3k; z=2k
x^2-y^2-z^2=4
=>16k^2-9k^2-4k^2=4
=>3k^2=4
=>k^2=4/3
TH1: \(k=\dfrac{2\sqrt{3}}{3}\)
=>\(x=\dfrac{8\sqrt{3}}{3};y=\dfrac{2\sqrt{3}}{3}\cdot3=2\sqrt{3};z=\dfrac{4\sqrt{3}}{3}\)
TH2: \(k=\dfrac{2\sqrt{3}}{3}\)
\(x=\dfrac{-8\sqrt{3}}{3};y=\dfrac{-2\sqrt{3}}{3}\cdot3=-2\sqrt{3};z=\dfrac{-4\sqrt{3}}{3}\)
3: x/2=y/3 nên x/10=y/15
y/5=z/7 nên y/15=z/21
=>x/10=y/15=z/21
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}=\dfrac{x+y+z}{10+15+21}=\dfrac{23}{46}=\dfrac{1}{2}\)
=>x=5; y=7,5; z=10,5