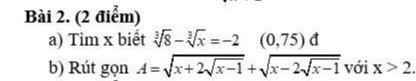Question

Answer 1

Bài 2

\(A=\sqrt{x-1+2\sqrt{x-1}+1}+\sqrt{x-1-2\sqrt{x-1}+1}\\ =\sqrt{\left[\left(\sqrt{x-1}\right)+1\right]^2}+\sqrt{\left[\left(\sqrt{x-1}-1\right)\right]^2}\\ =\sqrt{x-1}+1+\sqrt{x-1}-1\\ =2\sqrt{x-1}\)

Answer 2

Bài `2`:

`a, 2 -` \(\sqrt[3]{x}\) `=-2`

`->` \(\sqrt[3]{x}\) `= 4`

`-> x = 64`

Answer 3

`a)\root[3]{8}-\root[3]{x}=-2`

`<=>2-\root[3]{x}=-2`

`<=>\root[3]{x}=4`

`<=>x=64`

Vậy `x=64`

______________________________________

`b)` Với `x > 2` có:

`A=\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}`

`A=\sqrt{x-1+2\sqrt{x-1}+1}+\sqrt{x-1-2\sqrt{x-1}+1}`

`A=\sqrt{(\sqrt{x-1}+1)^2}+\sqrt{(\sqrt{x-1}-1)^2}`

`A=|\sqrt{x-1}+1|+|\sqrt{x-1}-1|`

`A=\sqrt{x-1}+1+|\sqrt{x-1}-1|` (Với `x > 2`)

 Mà `x > 2<=>x-1 > 1<=>\sqrt{x-1} > 1<=>\sqrt{x-1}-1 > 0=>|\sqrt{x-1}-1|=\sqrt{x-1}-1`

  `=>A=\sqrt{x-1}+1+\sqrt{x-1}-1=2\sqrt{x-1}`