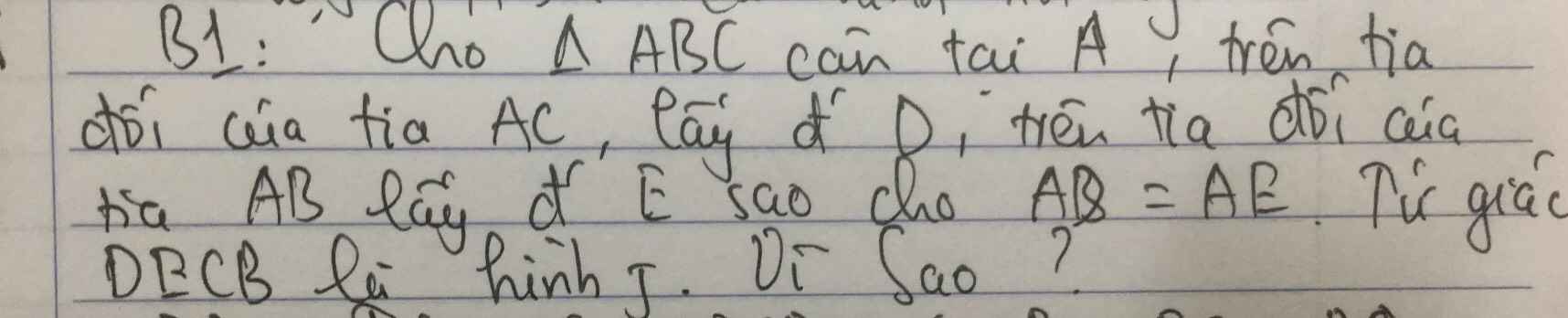Vì `\triangle ABC` cân tại `A=>{(AB=AC),(\hat{ABC}=\hat{ACB}):}`
Có: `[AD]/[AC]=[AE]/[AB]`
`=>DE //// BC` (Định lí Ta-lét đảo)
`=>` T/g `DECB` là hình thang `(1)`
Ta có: `AD+AC=DC`
`AE+AB=EB`
Mà `AD=AE;AC=AB`
`=>DC=EB`
Xét `\triangle DBC` và `\triangle ECB` có:
`{:(DC=EB),(\hat{DCB}=\hat{EBC}),(BC\text{ là cạnh chung}):}}=>`
`=>\triangle DBC =\triangle ECB` (c-g-c)
`=>\hat{DBC}=\hat{ECB}` `(2)`
Từ `(1);(2)=>` T/g `DECB` là hình thang cân
Đúng 1
Bình luận (2)
