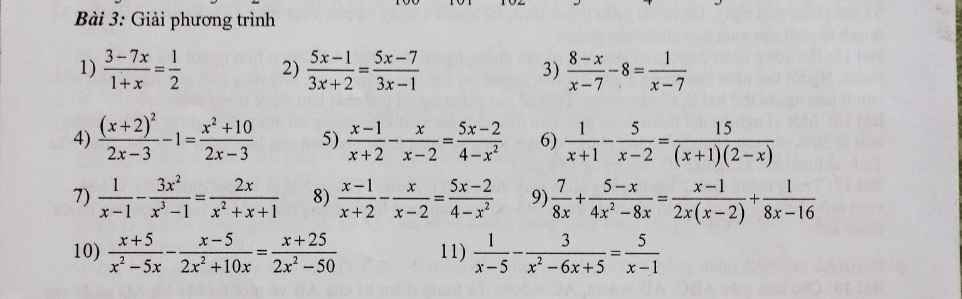1: =>6-14x=x+1
=>-15x=-5
=>x=1/3
2: =>(5x-1)(3x-1)=(5x-7)(3x+2)
=>15x^2-8x+1=15x^2+10x-21x-14
=>-8x+1=-11x-14
=>3x=-15
=>x=-5
3: =>\(\dfrac{8-x-8x+56}{x-7}=\dfrac{1}{x-7}\)
=>-9x+64=1
=>-9x=-63
=>x=7(loại)
5: =>\(\dfrac{x^2-3x+2-x^2-2x}{\left(x+2\right)\left(x-2\right)}=\dfrac{-5x+2}{\left(x-2\right)\left(x+2\right)}\)
=>-5x+2=-5x+2
=>0x=0(luôn đúng)
=>\(x\in R\backslash\left\{2;-2\right\}\)
6: =>\(\dfrac{x-2-5x-5}{\left(x+1\right)\left(x-2\right)}=\dfrac{-15}{\left(x+1\right)\left(x-2\right)}\)
=>-4x-7=-15
=>-4x=-8
=>x=2(loại)
7: =>\(x^2+x+1-3x^2=2x\left(x-1\right)\)
=>-2x^2+x+1=2x^2-2x
=>3x=-1
=>x=-1/3(nhận)
8: =>\(\dfrac{x^2-3x+2-x^2-2x}{\left(x-2\right)\left(x+2\right)}=\dfrac{-5x+2}{\left(x-2\right)\left(x+2\right)}\)
=>-5x+2=-5x+2
=>0x=0(luôn đúng)
Vậy S=R\{2;-2}