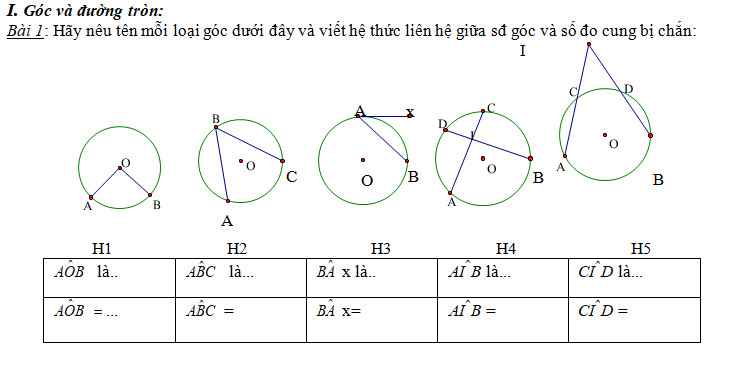
\(H1\)
\(+\widehat{AOB}\) là góc ở tâm
\(+\widehat{AOB}=\) số đo \(\stackrel\frown{AB}\)
\(H2\)
\(+\widehat{ABC}\) là góc nội tiếp
\(+\widehat{ABC}=\dfrac{1}{2}\)số đo \(\stackrel\frown{AC}\)
\(H3\)
\(+\widehat{BAx}\) là góc tạo bởi tiếp tuyến và dây cung
\(+\widehat{BAx}=\dfrac{1}{2}\)số đo \(\stackrel\frown{AB}\)
\(H4\)
\(+\widehat{AIB}\) là góc nội tiếp
\(+\widehat{AIB}=\dfrac{1}{2}\)số đo \(\stackrel\frown{AB}\)
\(H5\)
\(+\widehat{CID}\) là góc có đỉnh ngoài đường tròn
\(+\widehat{CID}=\)số đo \(\stackrel\frown{CD}\) và số đo \(\stackrel\frown{AB}\)