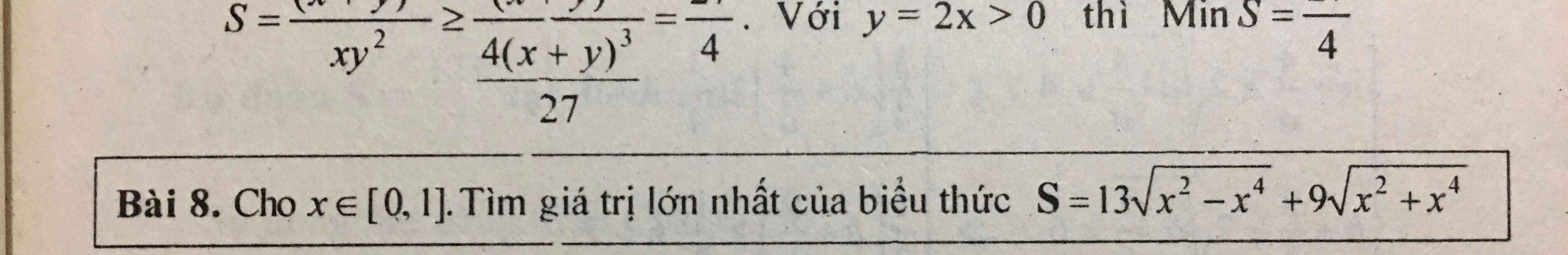Ta có: $S=\sqrt{13}.\sqrt{13}.\sqrt{x^2-x^4}+3.\sqrt{3}.\sqrt{3}.\sqrt{x^2+x^4}$
Áp dụng bất đẳng thức $Bunhiacopxki$ ta được:
$S^2 \le \left ( 13+27 \right ).\left [ 13(x^2-x^4)+3(x^2+x^4) \right ]=40x^2(16-10x^2)=4.\frac{(10x^2-10x^2+16)^2}{4}=256$
$\Leftrightarrow S \le 16$
Dấu $"="$ xảy ra khi: $x=\frac{2}{\sqrt{5}}$
cho a,b,c ∈ [0 ; 1]. Cmr: \(\frac{a}{b+c+1}+\frac{b}{a+c+1}+\frac{c}{a+b+1}+\left(1-a\right)\left(1-b\right)\left(1-c\right)\le1\)
bài 17 với 22
Biết tổng 2 số không âm là 82. Tìm GTLN và GTNN của tổng bình phương của chúng.
cần giải thuchs dòng thứ 4 huhu
Cho \(x>0,y>0\)
CMR: \(\dfrac{x+y}{2}\ge\dfrac{2}{\dfrac{1}{x}+\dfrac{1}{y}}\)
Cho a, b, c, d là những số dương.
Chứng minh rằng :
\(\dfrac{a}{\sqrt{b}}+\dfrac{b}{\sqrt{a}}\ge\sqrt{a}+\sqrt{b}\)
cho a, b, c là 3 số thực dương. cmr \(\frac{a^2}{b^2c}+\frac{b^2}{c^2a}+\frac{c^2}{a^2b}\ge\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)
Cho x,y,z > 0 có xy+yz+xz = 3xyz CMR : \(\dfrac{x^3}{x^2+z}+\dfrac{y^3}{y^2+x}+\dfrac{z^3}{z^2+y}\ge\dfrac{1}{2}\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)\)
Giúp mình gấp câu này,căn quá à: Cho x,y,z>0 và x+y+z=1 tìm GTNN( min) của \(P=\frac{9}{1-\left(xy+yz+zx\right)}+\frac{1}{4xyz}\)
Cho tam giác ABC có chu vi bằng 2. Kí hiệu a, b, c, là độ dài ba cạnh của tam giác.Tìm giá trị nhỏ nhất của biểu thức
\(S=\frac{a}{b+c-a}+\frac{b}{a+c-b}+\frac{c}{a+b-c}\)
Gíup mình với mọi người !!!!!
