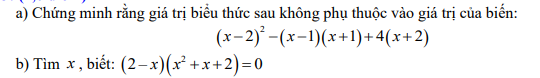Question

Answer 1

\(a,\left(x-2\right)^2-\left(x-1\right)\left(x+1\right)+4\left(x+2\right)\\ =x^2-4x+4-x^2+1+4x+8\\ =13\)

\(b,\left(2-x\right)\left(x^2+x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2-x=0\\x^2+x+2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{7}{4}=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\\left(x+\dfrac{1}{2}\right)^2+\dfrac{7}{4}=0\left(vô.lí\right)\end{matrix}\right.\)

Vậy x=2

Answer 2

b: =>2-x=0

hay x=2

a: \(=x^2-4x+4-x^2+1+4x+8=13\)

Answer 3

a) (x-2)²-(x-1)(x+1)+4(x+2)
= x²-4x+4-x²+1+4x+8
= (x²-x²)+(-4x+4x)+(4+1+8)
= 13
Vậy giá trị biểu thức trên không phụ thuộc vào biến.
b) (2-x)(x²+x+2)=0
Th1: 2-x=0           Th2: x²+x+2=0
           x=2                    x²+x=-2 (loại)
Vậy x=2