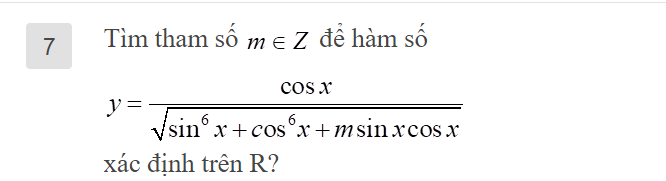Hàm xác định trên R khi với mọi x ta có:
\(sin^6x+cos^6x+m.sinx.cosx>0\)
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)+\dfrac{m}{2}sin2x>0\)
\(\Leftrightarrow1-\dfrac{3}{4}sin^22x+\dfrac{m}{2}sin2x>0\)
Đặt \(sin2x=t\in\left[-1;1\right]\)
\(\Rightarrow-3t^2+2m.t+4>0\)
\(\Leftrightarrow\min\limits_{\left[-1;1\right]}f\left(t\right)>0\)
Xét hàm \(f\left(t\right)=-3t^2+2mt+4\) có \(a=-3< 0\) ; \(-\dfrac{b}{2a}=\dfrac{m}{3}\) ;
\(f\left(-1\right)=1-2m\) ; \(f\left(1\right)=1+2m\)
TH1: \(\dfrac{m}{3}\le-1\Rightarrow m\le-3\)
\(\Rightarrow\min\limits_{\left[-1;1\right]}f\left(t\right)=f\left(1\right)=1+2m>0\Rightarrow m>-\dfrac{1}{2}\) (ktm)
TH2: \(\dfrac{m}{3}\ge1\Rightarrow m\ge3\)
\(\Rightarrow\min\limits_{\left[-1;1\right]}f\left(t\right)=f\left(-1\right)=1-2m>0\Rightarrow m< \dfrac{1}{2}\) (ktm)
TH3: \(-1< \dfrac{m}{3}< 1\Rightarrow-3< m< 3\)
\(\Rightarrow\min\limits_{\left[-1;1\right]}f\left(t\right)=min\left\{1-2m;1+2m\right\}\)
TH3.1: \(\left\{{}\begin{matrix}1-2m\le1+2m\\1-2m>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ge0\\m< \dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow0\le m< \dfrac{1}{2}\)
TH3.2: \(\left\{{}\begin{matrix}1+2m\le1-2m\\1+2m>0\end{matrix}\right.\) \(\Rightarrow-\dfrac{1}{2}< m\le0\)
Kết hợp lại ta được: \(-\dfrac{1}{2}< m< \dfrac{1}{2}\)