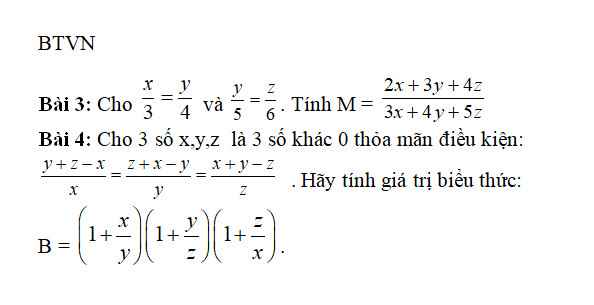\(\dfrac{x}{3}=\dfrac{y}{4}\Rightarrow\dfrac{x}{15}=\dfrac{y}{20}\\ \dfrac{y}{5}=\dfrac{z}{6}\Rightarrow\dfrac{y}{20}=\dfrac{z}{24}\\ \Rightarrow\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{24}\)
Đặt \(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{24}=k\Rightarrow x=15k,y=20k,z=24k\)
\(M=\dfrac{2x+3y+4z}{3x+4y+5z}=\dfrac{2.15k+3.20k+4.24k}{3.15k+4.20k+5.24k}=\dfrac{30k+60k+96k}{45k+80k+120k}=\dfrac{186k}{245k}=\dfrac{186}{245}\)
Bài 4:
TH1: \(x+y+z=0\Rightarrow\left\{{}\begin{matrix}x+y=-z\\y+z=-x\\z+x=-y\end{matrix}\right.\)
\(B=\left(1+\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\left(1+\dfrac{z}{x}\right)\)
\(\Rightarrow B=\dfrac{x+y}{y}.\dfrac{y+z}{z}.\dfrac{z+x}{x}\)
\(\Rightarrow B=\dfrac{-z}{y}.\dfrac{-x}{z}.\dfrac{-y}{x}\)
\(\Rightarrow B=-1.\left(-1\right).\left(-1\right)\)
\(\Rightarrow B=-1\)
TH2:\(x+y+z\ne0\)
Áp dụng t/c dtsbn ta có:
\(\dfrac{y+z-x}{x}=\dfrac{z+x-y}{y}=\dfrac{x+y-z}{z}=\dfrac{y+z-x+z+x-y+x+y-z}{x+y+z}=\dfrac{x+y+z}{x+y+z}=1\)
\(\dfrac{y+z-x}{x}=1\Rightarrow y+z-x=x\Rightarrow y+z=2x\\ \dfrac{z+x-y}{y}=1\Rightarrow x+z-y=y\Rightarrow x+z=2y\\ \dfrac{x+y-z}{z}=1\Rightarrow x+y-z=z\Rightarrow x+y=2z\)
\(B=\left(1+\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\left(1+\dfrac{z}{x}\right)\)
\(\Rightarrow B=\dfrac{x+y}{y}.\dfrac{y+z}{z}.\dfrac{z+x}{x}\)
\(\Rightarrow B=\dfrac{2z}{y}.\dfrac{2x}{z}.\dfrac{2y}{x}\)
\(\Rightarrow B=2.2.2\)
\(\Rightarrow B=8\)