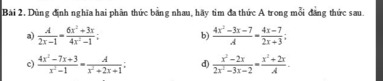\(a,A=\dfrac{\left(6x^2+3x\right)\left(2x-1\right)}{4x^2-1}=\dfrac{3x\left(2x+1\right)\left(2x-1\right)}{\left(2x+1\right)\left(2x-1\right)}=3x\\ b,A=\dfrac{\left(4x^2-3x-7\right)\left(2x+3\right)}{4x-7}=\dfrac{\left(x+1\right)\left(4x-7\right)\left(2x+3\right)}{4x-7}=\left(x+1\right)\left(2x+3\right)\\ c,A=\dfrac{\left(4x^2-7x+3\right)\left(x^2+2x+1\right)}{x^2-1}=\dfrac{\left(x-1\right)\left(4x-3\right)\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}=\left(4x-3\right)\left(x+1\right)\\ d,A=\dfrac{\left(2x^2-3x-2\right)\left(x^2+2x\right)}{x^2-2x}=\dfrac{x\left(x+2\right)\left(x-2\right)\left(2x+1\right)}{x\left(x-2\right)}=\left(x+2\right)\left(2x+1\right)\)
Bài 1: Phân thức đại số.
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
√x^2-4+√x+2
tìm đkxđ giải chi tiết nha
ĐỀ TOÁN: Quãng đường AB dài 108km. Một ô tô khởi hành từ A lúc 7 gio10 phút và đến B là lúc 10 giờ. Tìm vận tốc của ô tô, biết giữa đường ô tô nghỉ hết 35 phút.
Tìm x biết: ( x + 5 ) ( x - 1 ) = 2x ( x + 5 )
Phân tích đa thức thành nhân tử:
a) 4x^4+1
b) 4x^4 +y^4
c) x^4+ 324
d) (x+2)(x+3)(x+4)(x+5)-24
e)x^3-6x^2-x+30
Các bạn giúp mình với nào!!! Mình đang cần gấp nhé!

P= (\(\dfrac{2+x}{2-x}+\dfrac{4x^2}{x^2-4}-\dfrac{2-x}{2+x}\)):\(\dfrac{x^2-3x}{2x^2-x^3}\)
a)Tìm ĐKXĐ
Rút gọn P
b)Tính gt của S vs /x-5/ =2
d)Tìm x để gt của x để p <0
(x2 - 2x + 4)(x + 2) - x(x2 + 2) = 17
CM đẳng thức:
\(\dfrac{x^2y\:+\:2xY\:^2+y^3}{2x^2+xY\:-y^2}\:=\:\dfrac{xY\:+\:y^2}{2x-y}\)
Bài 1:Cho biểu thức:
\(A=\dfrac{2}{x-1}+\dfrac{2\left(x+1\right)}{x^2+x+1}+\dfrac{x^2-10x+3}{x^3-1}\)
a)Tìm đkxđ của A
b)rút gọn A
c)tìm GTNN của A
Giúp mk với mk đang cần gấp.
1)Thực hiện phép tính :
a) \(\dfrac{x^2-y^2}{x^3}+y^3.\left[\left(x-\dfrac{x^2+y^2}{y}\right):\left(\dfrac{1}{x}-\dfrac{1}{y}\right)\right]\)
2) CMR nếu \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=\dfrac{1}{x+y+z}\)
thì \(\dfrac{1}{x^5}+\dfrac{1}{y^5}+\dfrac{1}{z^5}=\dfrac{1}{x^5+y^5+z^5}\).