Xét hàm \(f\left(x\right)=x^3-3x\)
\(f'\left(x\right)=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=-1\Rightarrow y=2\\x=1\Rightarrow y=-2\end{matrix}\right.\)
BBT:
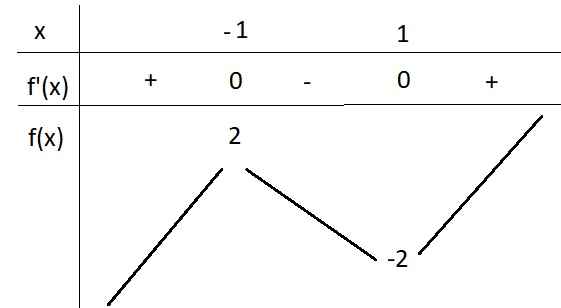
Từ BBT ta thấy \(y=3m-m^3\) cắt \(y=f\left(x\right)\) tại 3 điểm pb khi:
\(-2< 3m-m^3< 2\)
\(\Rightarrow\left\{{}\begin{matrix}\left\{{}\begin{matrix}m< 2\\m\ne-1\end{matrix}\right.\\\left\{{}\begin{matrix}m>-2\\m\ne1\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-2< m< 2\\m\ne\pm1\end{matrix}\right.\)