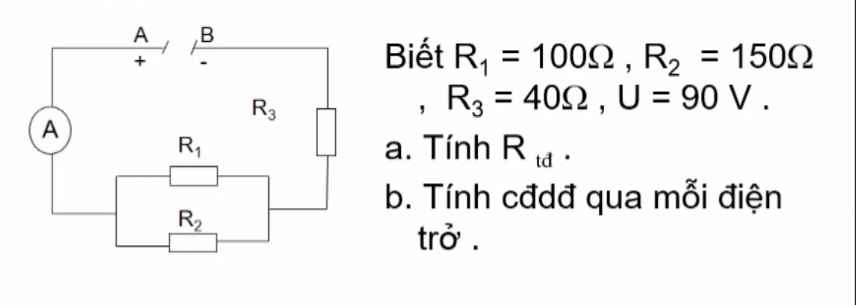
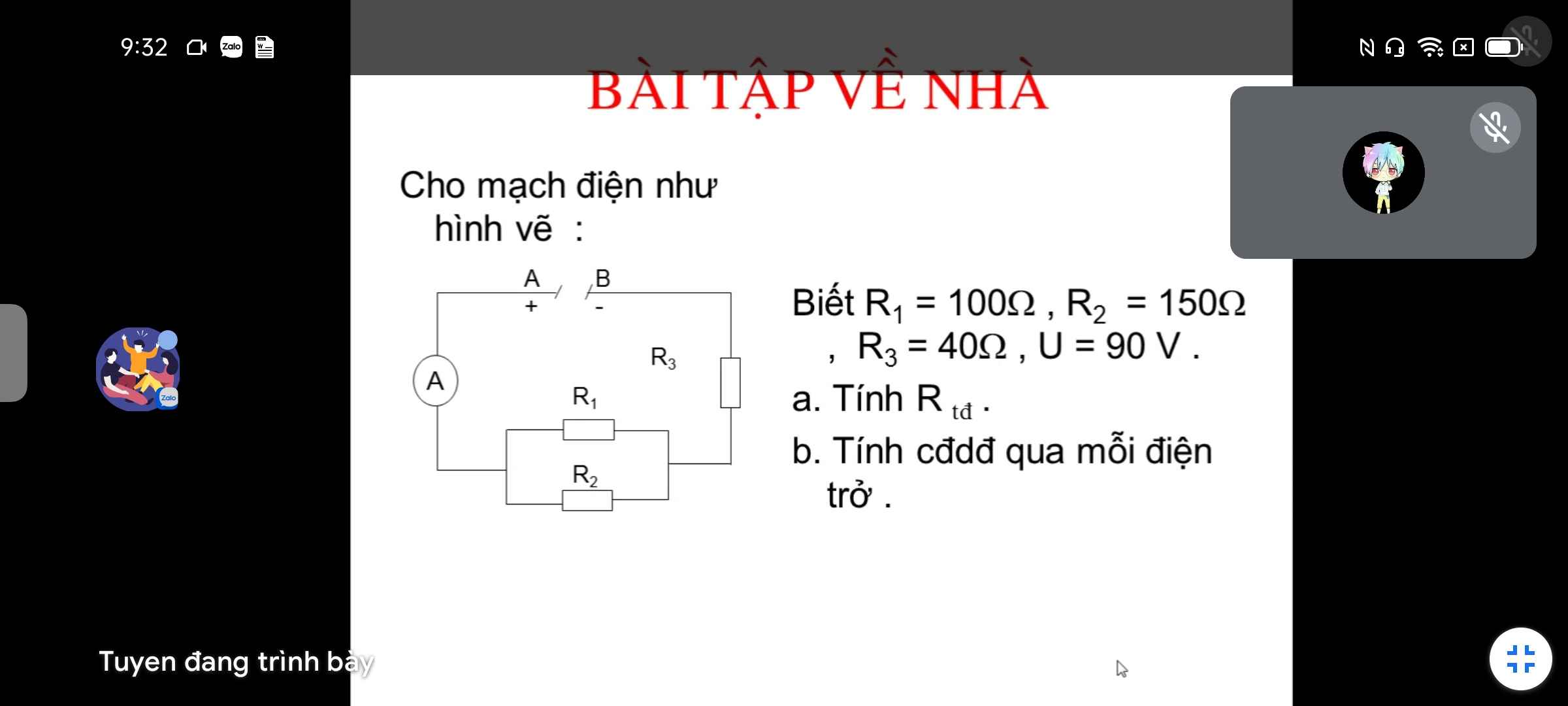
a) R1//R2
\(\Rightarrow R_{12}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{100.150}{100+150}=60\left(\Omega\right)\)
\(R_{tđ}=R_{12}+R_3=60+40=100\left(\Omega\right)\)
b) \(I=I_3=I_{12}=\dfrac{U}{R_{tđ}}=\dfrac{90}{100}=0,9\left(A\right)\)
\(U_{12}=U_1=U_2=I_{12}.R_{12}=0,9.60=54\left(V\right)\)
\(\left\{{}\begin{matrix}I_1=\dfrac{U_1}{R_1}=\dfrac{54}{100}=0,54\left(A\right)\\I_2=\dfrac{U_2}{R_2}=\dfrac{54}{150}=0,36\left(A\right)\end{matrix}\right.\)
Đúng 3
Bình luận (0)
