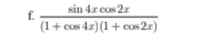Chương 6: CUNG VÀ GÓC LƯỢNG GIÁC. CÔNG THỨC LƯỢNG GIÁC
Các câu hỏi tương tự
Cho sin3x - cos3x = \(\frac{\sqrt{2}}{2}\)
Tính giá trị của biểu thức : A= tan \(\left(x+\frac{\pi}{4}\right)\)
cho tam giác ABC thỏa mãn điều kiện \(p.tan\frac{B}{2}tan\frac{C}{2}=p-c\) Chứng mình tam giác cân tại B
Chứng minh đẳng thức sau:
\(\left(\frac{sinx+cotx}{1+sinx.tanx}\right)^n\) =\(\frac{sin^nx+cot^nx}{1+sin^nx.tan^nx}\)
Cho \(\sin a+\cos a=\frac{5}{4}\)
a, Tính \(\sin a\times\cos a\)
b, tính \(\sin a-\cos a\)
Bài 1 a) Số giá trị nguyên của tham số m thuộc [-5;5] để phương trình : x2+2mx+m2+m−30 để phương trình có 2 nghiệm phân biệt.
b) Với giá trị nào của m thì nhị thức bậc nhất f(x) mx-3 luôn âm vs mọi x.
Bài 2
a) Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới 1 góc 78o24′ . Biết CA 250 m ,CB 120 m. Tính khoảng cách AB.
b) Một tam giác có ba cạnh là 13,14,15. Diện tích tam giác bằng bao nhiêu ?...
Đọc tiếp
Bài 1 a) Số giá trị nguyên của tham số m thuộc [-5;5] để phương trình : x2+2mx+m2+m−3=0 để phương trình có 2 nghiệm phân biệt.
b) Với giá trị nào của m thì nhị thức bậc nhất f(x)= mx-3 luôn âm vs mọi x.
Bài 2
a) Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới 1 góc 78o24′ . Biết CA =250 m ,CB = 120 m. Tính khoảng cách AB.
b) Một tam giác có ba cạnh là 13,14,15. Diện tích tam giác bằng bao nhiêu ?
c) Cho hai điểm A (-3;2) , b (4;3) .Tìm điểm M thuộc trục Ox và có hoành độ dương để tam giác MAB vuông tại M.
Cho A(2;2) và 2 đường thẳng d1:x+y-2=0 , d2: x+y-8=0 Tìm B thuộc d1, C thuộc d2 sao cho tam giác ABC vuông cân tại A
4 tháng 7 2021 lúc 20:06
Xác định dạng của ΔABC biết
\(\sqrt[n]{sinA}+\sqrt[n]{sinB}=2\sqrt[n]{cos\dfrac{C}{2}}\)
29 tháng 6 2021 lúc 20:47
Xác định dạng của ΔABC biết
\(\sqrt{sinA}+\sqrt{sinB}=2\sqrt{cos\dfrac{C}{2}}\)
Bài 1: Rút gọn:
A= \(\dfrac{sin2\alpha+sin\alpha}{1+cos2\alpha+cos2\alpha}\)
B= \(\dfrac{4sin^2\alpha}{1-cos^2\dfrac{\alpha}{2}}\)
C= \(\dfrac{1+cos\alpha-sin\alpha}{1-cos\alpha-sin\alpha}\)
Rút gọn 