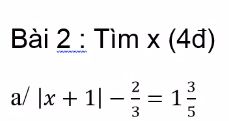Question

Answer 1

⇔ \(|x+1|-\dfrac{2}{3}=\dfrac{8}{5} \)

⇔ \(|x+1|=\dfrac{34}{15} \)

⇒ \(\left[{}\begin{matrix}x=\dfrac{19}{15}\\x=-\dfrac{49}{15}\end{matrix}\right.\)

Answer 2

|x+1| - \(\dfrac{2}{3}\)= 1\(\dfrac{3}{5}\)

|x+1| = 1\(\dfrac{3}{5}\) + \(\dfrac{2}{3}\)

|x+1| =  \(\dfrac{34}{15}\)

⇒ x+1 = \(\dfrac{34}{15}\) hoặc x+1 = \(\dfrac{-34}{15}\)

 ⇒ x = \(\dfrac{34}{15}\) - 1 hoặc x = \(\dfrac{-34}{15}\) - 1

⇒ x = \(\dfrac{19}{15}\) hoặc x = \(\dfrac{-49}{15}\)