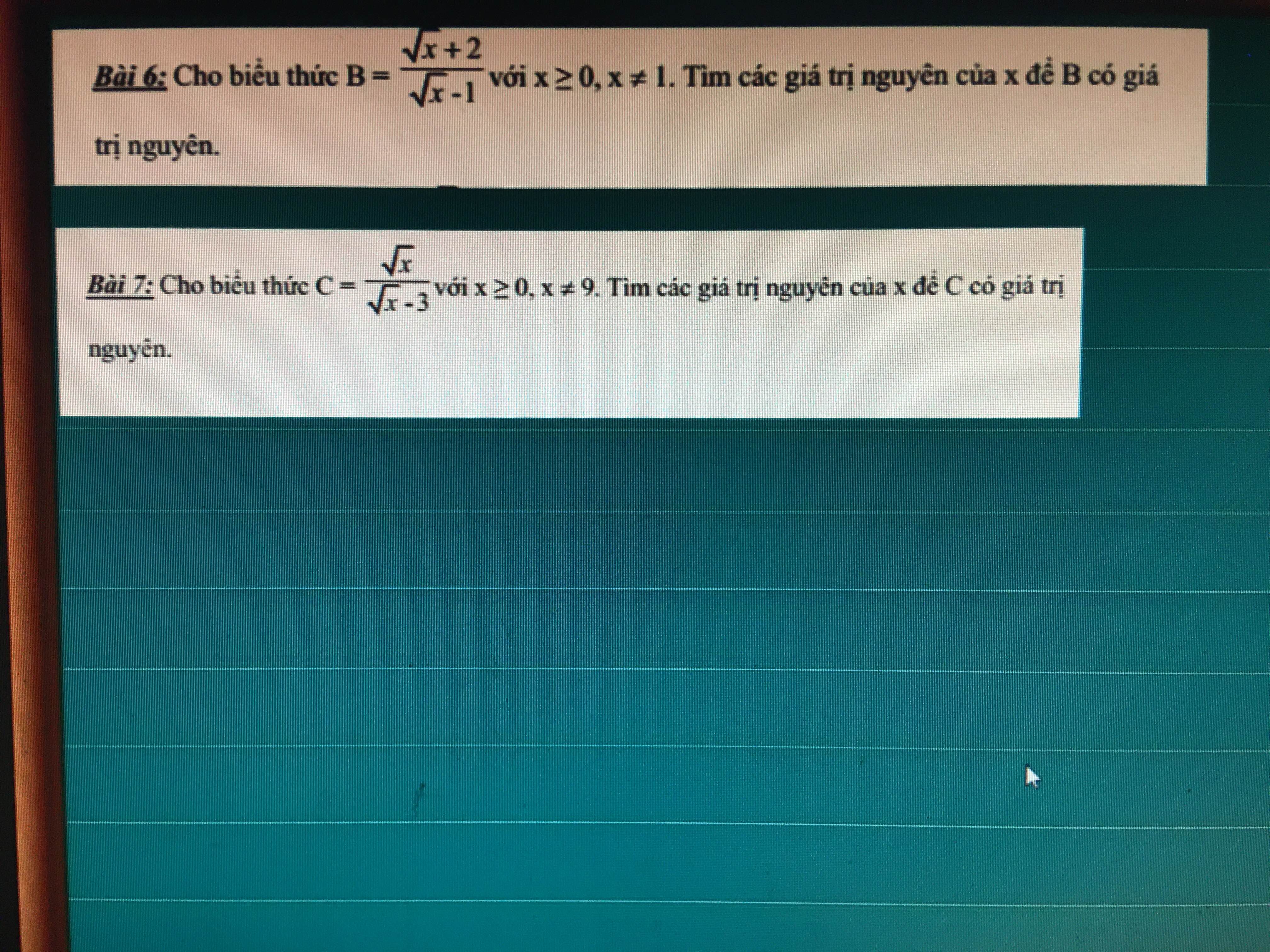
Bài 6:
\(B=\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\left(đk:x\ge0,x\ne1\right)=\dfrac{\sqrt{x}-1}{\sqrt{x}-1}+\dfrac{3}{\sqrt{x}-1}=1+\dfrac{3}{\sqrt{x}-1}\)
Để \(B\in Z\) thì: \(\sqrt{x}-1\inƯ\left(3\right)=\left\{1;-1;3;-3\right\}\)
Do \(x\in Z,x\ge0\)
\(\Rightarrow x\in\left\{4;0;16\right\}\)
Bài 17: \(C=\dfrac{\sqrt{x}}{\sqrt{x}-3}\left(đk:x\ge0,x\ne9\right)=\dfrac{\sqrt{x}-3}{\sqrt{x}-3}+\dfrac{3}{\sqrt{x}-3}=1+\dfrac{3}{\sqrt{x}-3}\)
Để \(C\in Z\) thì \(\sqrt{x}-3\inƯ\left(3\right)=\left\{1;-1;3;-3\right\}\)
Do \(x\in Z,x\ge0\)
\(\Rightarrow x\in\left\{16;4;36;0\right\}\)
6.
\(B\in Z\Leftrightarrow\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\in Z\)
\(\Leftrightarrow\dfrac{\sqrt{x}-1+3}{\sqrt{x}-1}\in Z\)
\(\Leftrightarrow1+\dfrac{3}{\sqrt{x}-1}\in Z\)
\(\Leftrightarrow\sqrt{x}-1\inƯ_3=\left\{\pm1;\pm3\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;2;4\right\}\)
\(\Leftrightarrow x\in\left\{0;4;16\right\}\)
Bài 7:
Để C nguyên thì \(\sqrt{x}⋮\sqrt{x}-3\)
\(\Leftrightarrow\sqrt{x}-3\in\left\{1;-1;3;-3\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{4;2;6;0\right\}\)
hay \(x\in\left\{0;4;16;36\right\}\)
Bài 6:
Để B nguyên thì \(3⋮\sqrt{x}-1\)
\(\Leftrightarrow\sqrt{x}-1\in\left\{-1;1;3\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;2;4\right\}\)
hay \(x\in\left\{0;4;16\right\}\)
7.
\(C\in Z\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}-3}\in Z\)
\(\Leftrightarrow\dfrac{\sqrt{x}-3+3}{\sqrt{x}-3}\in Z\)
\(\Leftrightarrow1+\dfrac{3}{\sqrt{x}-3}\in Z\)
\(\Leftrightarrow\sqrt{x}-3\inƯ_3=\left\{\pm1;\pm3\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;2;4;6\right\}\)
\(\Leftrightarrow x\in\left\{0;4;16;36\right\}\)